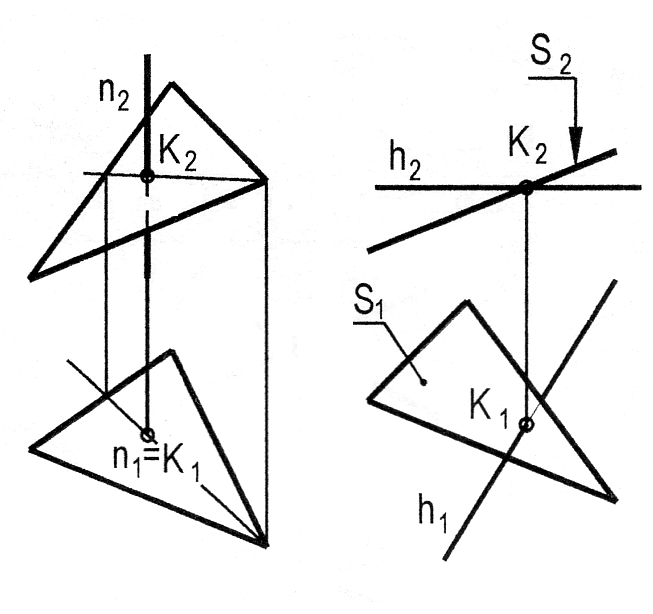
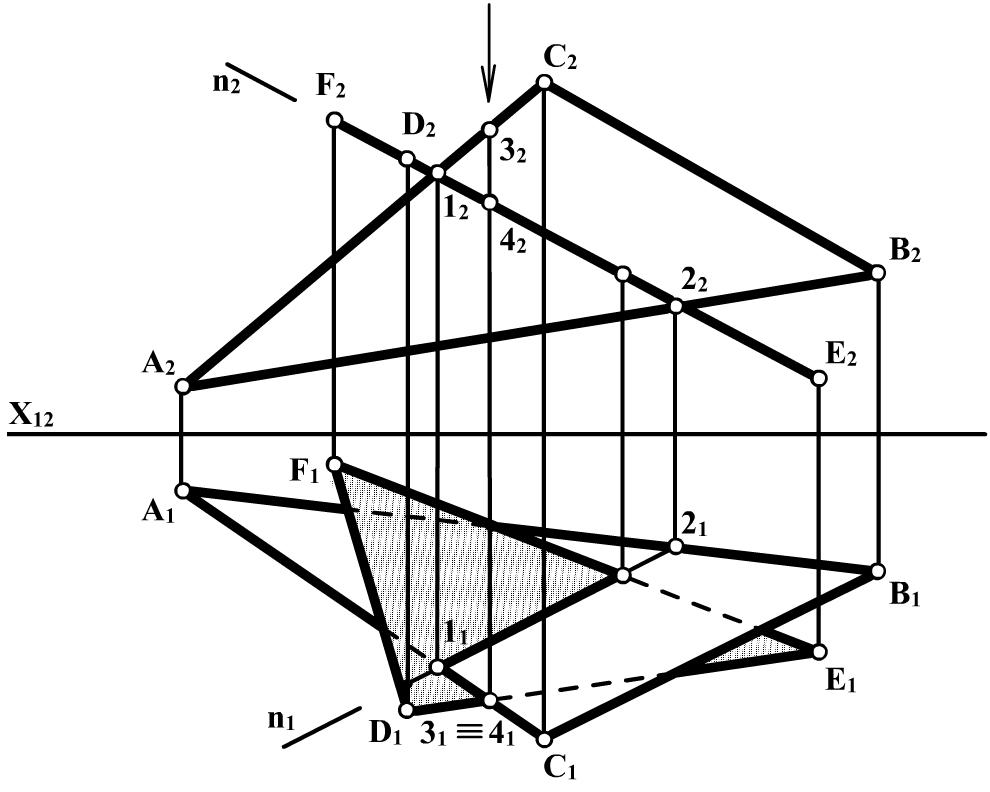
Перетин площини S проеціюючого положення з площиною Q

загального положення (рис. 3.19)

S ^ П₂, S(DDEF); Q(DАВС). S Ç Q = n. n Ì S; n Ì Q; n₂ º Q₂; пряму n фіксуємо двома точками – 1 і 2, які є спільними для обох площин, що перетинаються. Видимість площин Q і S визначаємо на П₁ за допомогою конкуруючих точок 3 і 4.

Рис. 3.19

 

Перетин прямої l загального положення з площиною S загального положення (рис. 3.20 і 3.21)

 

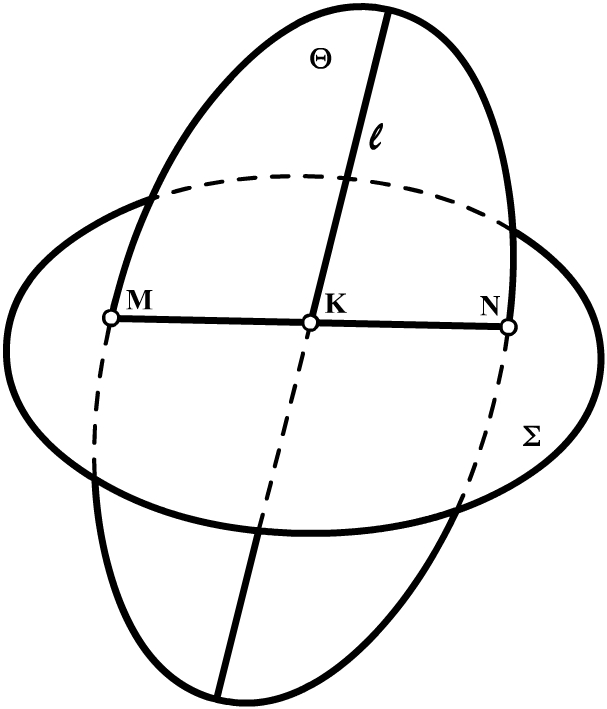
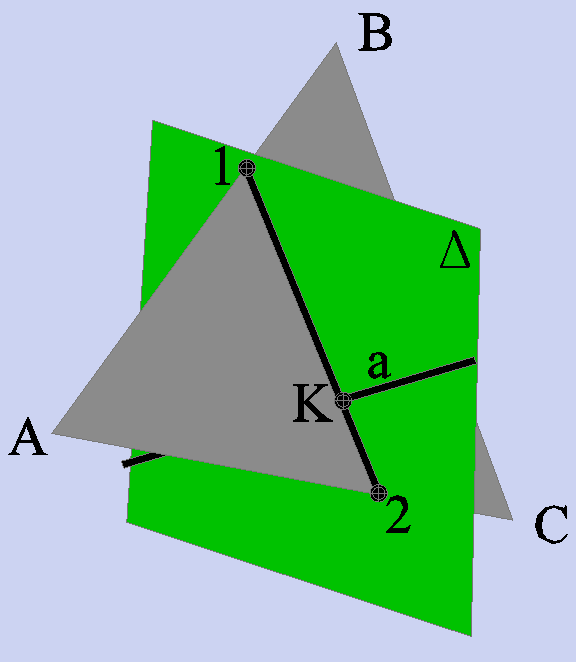
На рис. 3.20 зображені площина S і пряма l, що перетинається з цією площиною. Проведемо через пряму l площину Q. Якщо знайти пряму MN перетину площин S і Q, то точка перетину прямих l та MNбуде точкою, в якій пряма l перетинається з площиною S. Цю точку (К) часто називають точкою зустрічі прямої з площиною.

Таким чином, побудова точки зустрічі прямої загального положення з площиною загального положення складається з трьох операцій:

1) Проведення через задану пряму l допоміжної площини- посередника Q. Як допоміжні, звичайно, використовують проецію-ючі площини внаслідок простоти, з якою здійснюється проведення цих площин через прямі лінії на комплексному кресленні – завдяки збиральній властивості одного зі слідів-проекцій таких площин.

 

Рис. 3.19

 

2) Знаходження лінії MN перетину заданої площини S з допоміжною площиною посередником Q.

3) Визначення точки К перетину заданої прямої l зі знайденою лінією перетину двох площин. Точка К є шуканою точкою перетину прямої l з площиною S.

 

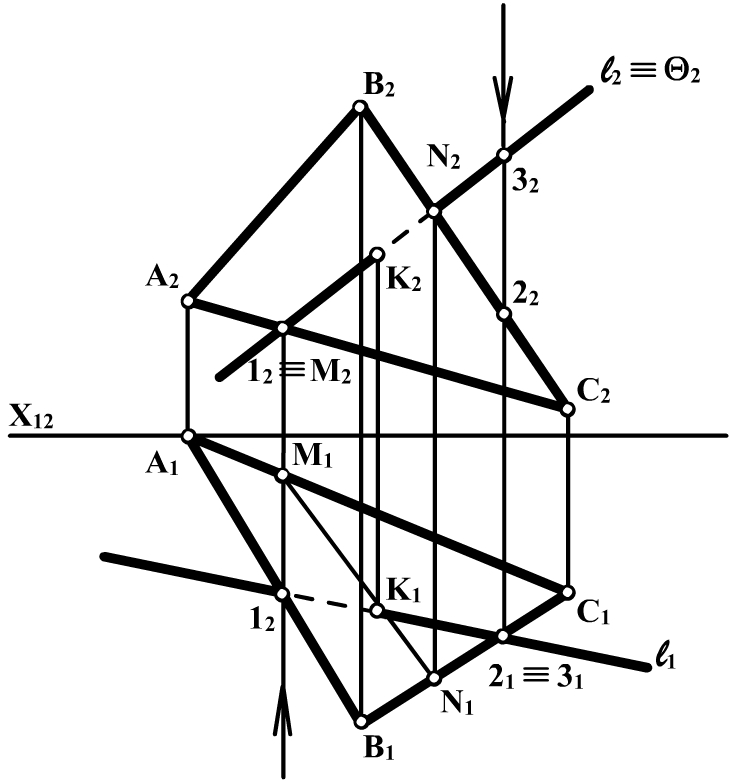
Рис. 3.20

 

На комплексному кресленні (рис. 3.20) задачу розв'язуємо в такому порядку:

1) l Ì Q; Q ^ P₂;

2) Q Ç S = MN; M Î AC; N Î BC;

3) MN Ç l = К; M₂N₂ º l₂; M₁N₁ Çl₁ = K₁; K₂ Î l₂.

4) Видимість прямої l по відношенню до площини S на П₁ і П₂ визначаємо за допомогою конкуруючих точок 1 i M; 2 і 3.

У таблиці 3.3 наведено приклади перетину прямої з площиною.

Таблиця 3.3

Перетин прямої з площиною

 

Пряма і площина займають загальне положення	Один елемент займає часткове положення	Пряма і площина займають часткове положення
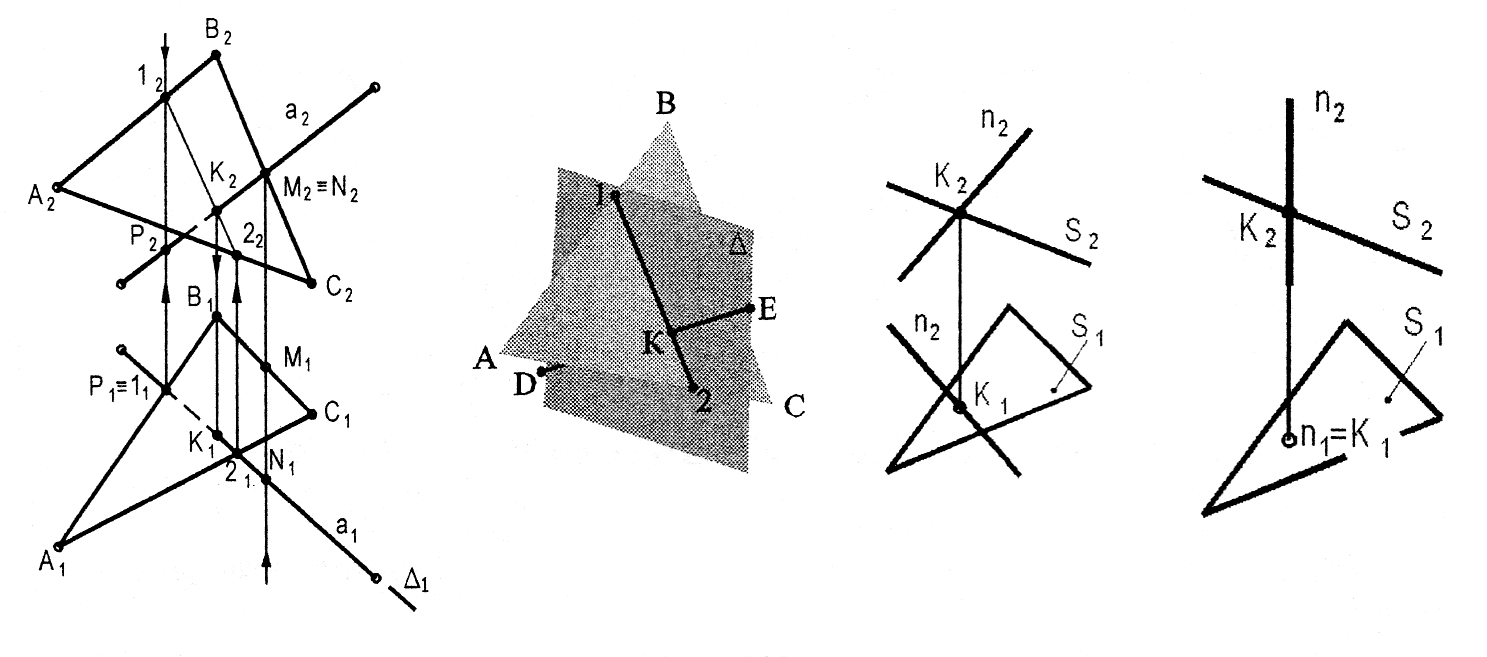
Алгоритм рішення: 1) а Ì D; D ^ P1; 2) D Ç S (DАВС) = 1-2; 1 Î AВ; 2 Î АC; 3) 1-2 Ç а = К; 1122 º а1; 1222 Ç а2 = K2; K2 Î а2; 4) Визначаємо видимість прямої та площини.