Прямі і точки, що лежать у площині

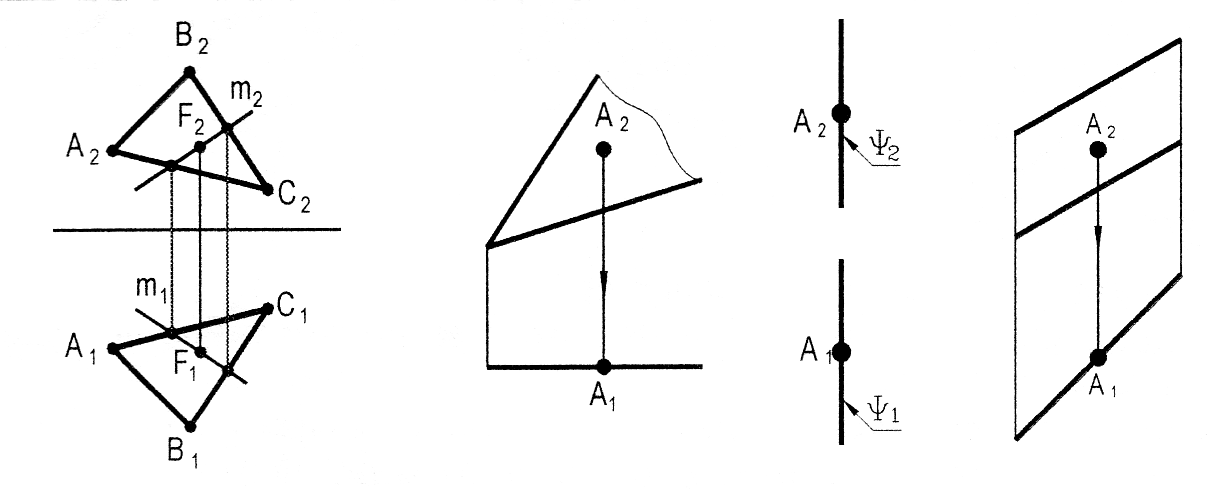
Пряма належить площині, якщо вона проходить через дві точки, що належать цій площині, або через одну її точку паралельно іншій прямій, проведеній на площині.

Приклад 1: Задана горизонтальна проекція прямої l(l₁), яка належить площині S(DАВС) - l É S. Побудувати відсутню фронтальну проекцію прямої l(l₂) (рис. 3.8).

Рис. 3.8

Приклад 2: Задано горизонтальну проекцію прямої k(k₁) і фронтальну проекцію прямої m(m₂). Прямі k i m належать площині Q(h⁰Çf⁰). Побудувати відсутні проекції прямих k i m (рис. 3.9).

Рис. 3.9

Точка належить площині, якщо вона лежить на прямій, що належить цій площині. Для визначення відсутньої проекції точки, яка лежить у площині необхідно спочатку побудувати проекції прямої, яка проходить через цю точку і лежить у площині і на цих проекціях прямої позначити проекції точки. У таблиці 3.1 наведено приклади належності точки площині.

Таблиця 3.1

Належність точки площині

Точка, яка належить площині загального положення	Точка, яка належить площині часткового положення
Рівня	Проеціюючій

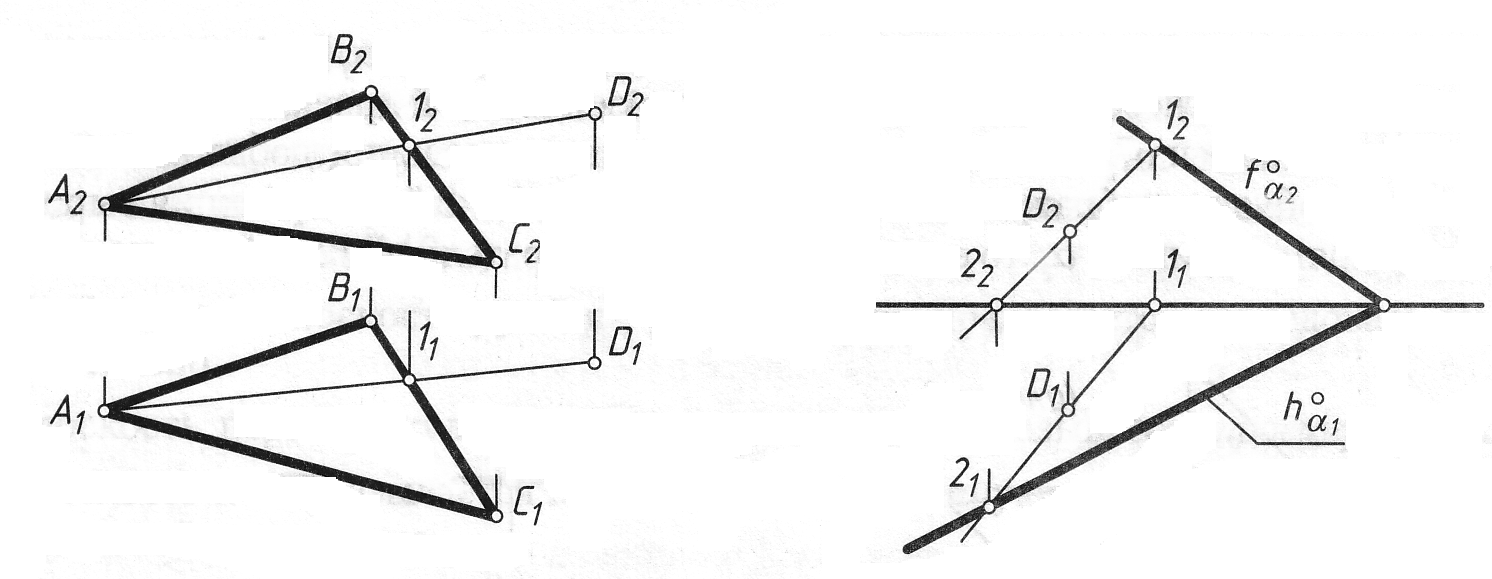
Приклад 3: Задана площина α(DАВС) та точка D(D₂)∈α. Необхідно знайти відсутню горизонтальну проекцію точки D₁ (рис. 3.10, а). Візьмемо у площині α пряму, яка проходить через точку D, наприклад її фронтальну проекцію (А₂D₂). Так як прямі (ВС) і (АD) знаходяться в одній площині, то точка 1=(ВС)Ç(АD) та 1₂=(В₂С₂)Ç(А₂D₂), а 1₁ знаходиться на лінії проеційного зв’язку (В₁С₁). Проведемо пряму лінію (А₁1₁) і на ній за лінією зв’язку знайдемо D₁.

а б

Рис. 3.10

Приклад 4: Задана площина α слідами та точка D(D₂)∈α. Необхідно знайти відсутню горизонтальну проекцію точки D₁ (рис. 4.10, б). Проведемо через точку D у площині α довільну пряму (1–2). Для цього через точку D₂ проведемо проекцію (1₂–2₂), побудуємо проекцію (1₁–2₁) і на ній за лінією зв’язку знайдемо D₁.