Спосіб обертання навколо проеціюючої прямої
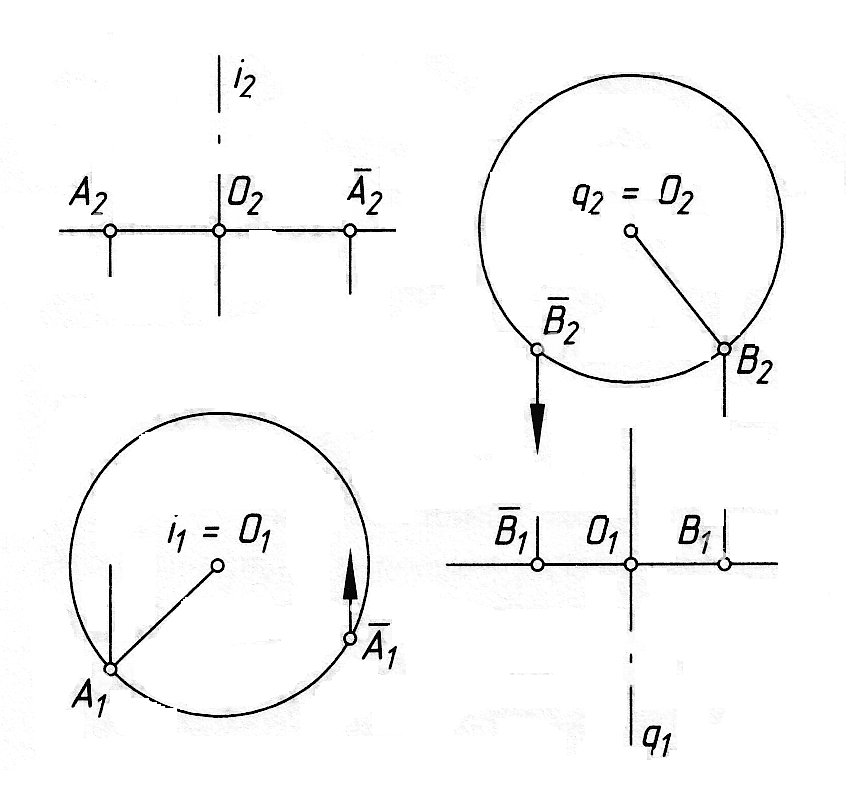
Частковим випадком плоско-паралельного переміщення є обертання фігури навколо осі, перпендикулярної до однієї з площин проекцій. При цьому всі точки фігури рухаються (переміщуються) по колах у площинах рівня, перпендикулярних до осі обертання. Центри кіл знаходяться в точках перетину осі із вказаними площинами. Якщо точка фігури знаходиться на осі обертання, то при обертанні системи ця точка вважається нерухомою. Таким чином, при обертанні навколо горизонтально-проеціюючої осі, фронтальні проекції точок фігури переміщуються по прямих, перпендикулярних до ліній зв'язку, а горизонтальні – по дугах кіл (рис. 4.11, а). Під час обертання навколо фронтально-проеціюючої прямої горизонтальні проекції точок переміщуються по прямих, перпендикулярних до ліній зв'язку, а фронтальні – по дугах кіл (рис. 4.11, б). Розв'язуючи задачі способами обертання, треба вміти показувати на кресленні такі основні елементи обертання: 1) Вісь обертання ί – пряму, навколо якої обертається точка. Вісь обертання (ί) беруть перпендикулярною до площин проекцій П1 або П2. 2) Площину обертання S, тобто площину, в якій переміщується точка і яка перпендикулярна до осі обертання ί.
а б
Рис. 4.11
Якщо вісь обертання перпендикулярна П1, то площина обертання буде горизонтальною. Якщо вісь обертання перпендикулярна П2, то площина обертання буде фронтальною. 3) Центр обертання – точка О перетину осі з площиною обертання О = S Ç ί. 4) Радіус обертання Rоб. – відстань точки від центра обертання. Радіус обертання проеціюється в натуральну величину на ту площину проекцій, перпендикулярно до якої вибрано вісь обертання.
Приклад 1. Перетворити пряму загального положення в проеціюючу пряму, визначити натуральну величину її відрізка АВ (рис. 4.12). Під час обертання прямої навколо осі доводиться обертати дві її точки. Побудова спрощується, якщо вісь обертання провести через одну з кінцевих точок відрізка: вісь ί проводимо через точку В q ^ П2. Щоб визначити натуральну величину відрізка АВ, обертаємо його фронтальну проекцію до положення паралельного Х12. Таким чином відрізок АВ став горизонталлю, а горизонтальна проекція `В1`А1 є його натуральною величиною. Для перетворення відрізка в проеціююче положення здійснюємо обертання відрізка АВ навколо горизонтально-проеціюючої осі ί (ί ^ П1). Обертаємо горизонтальну проекцію до положення `А1`В1 ^ Х12. Фронтальна проекція відрізка стане точкою: А 2 º В2.
Рис. 4.12
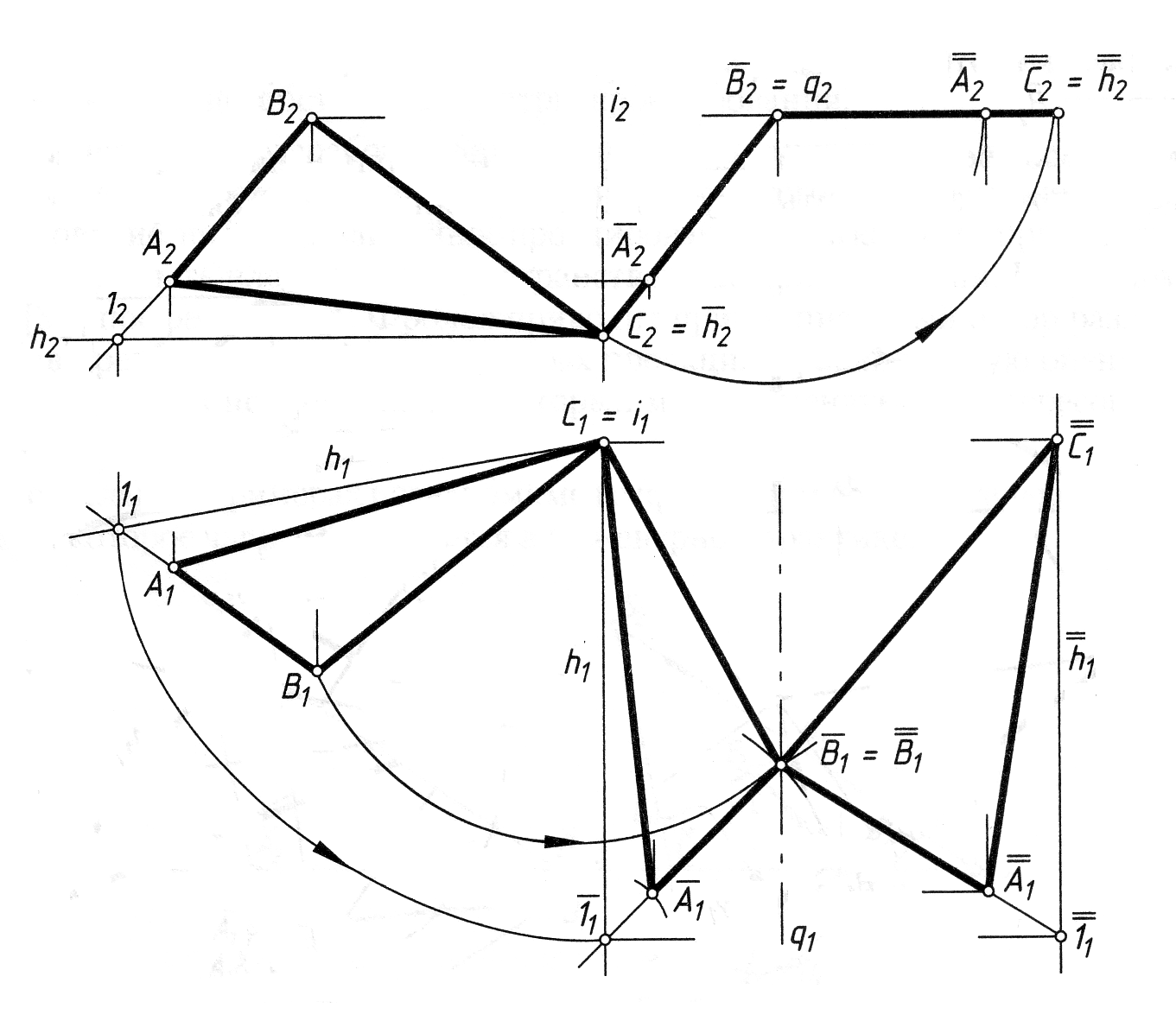
Приклад 2. Визначити натуральну величину DАВС. DАВС – площина загального положення (рис. 4.13).
Рис. 4.13
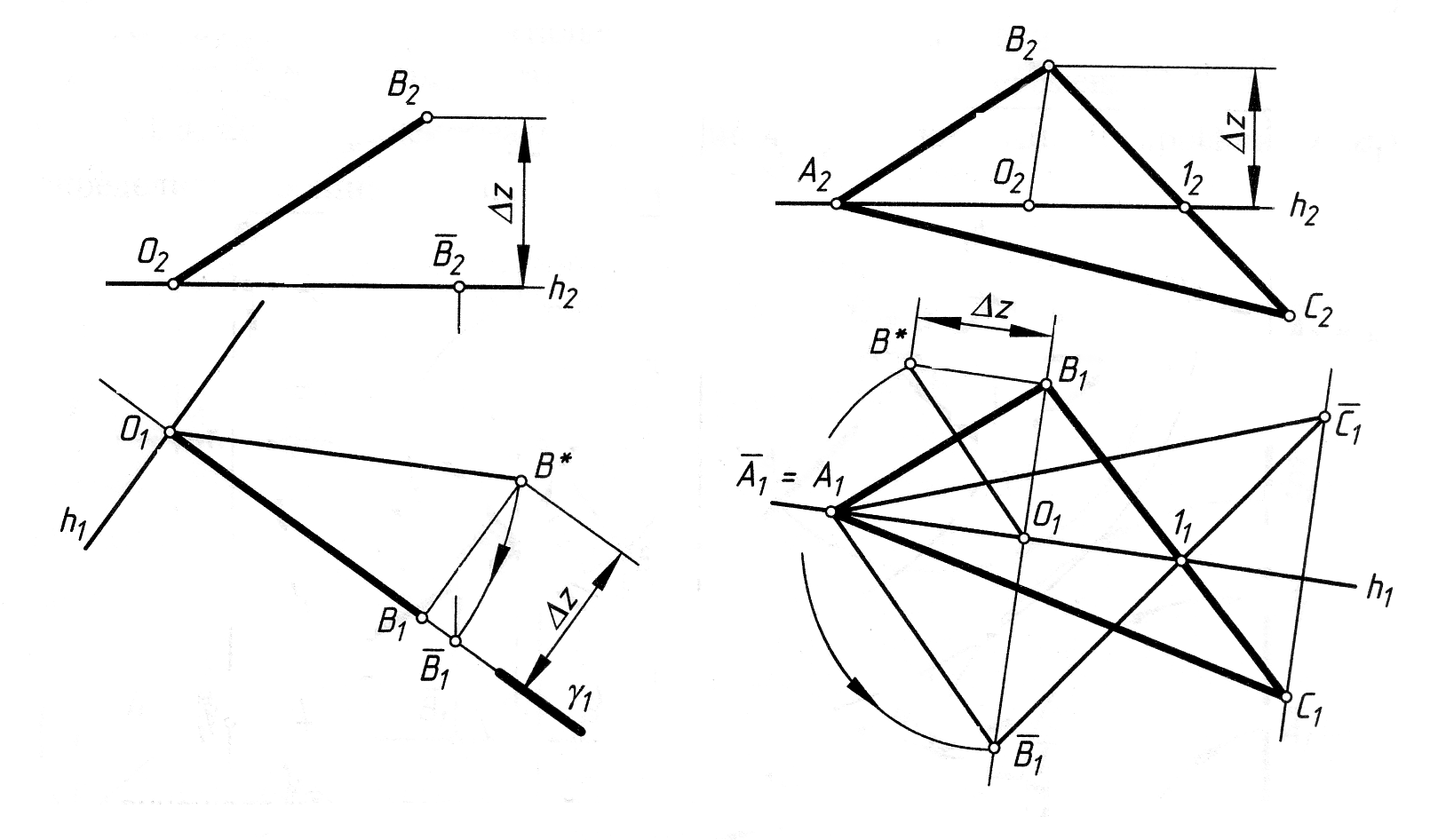
Перетворення виконуємо послідовним подвійним обертанням. Спочатку перетворюємо площину загального положення в проеціюючу площину. Для цього в площині DАВС проводимо одну із ліній рівня – h або f і обертаємо її до положення, коли вона стане перпендикулярною площині проекцій. При цьому лінія рівня спроеціюється в точку, а площина – в лінію. Потім площину обертаємо навколо іншої проеціюючої прямої до положення, коли площина стане паралельною площині проекцій. На цю площину вона спроеціюється в натуральну величину. Обертання навколо лінії рівня (спосіб суміщення) Обертання навколо горизонталі або фронталі застосовують, коли задану плоску фігуру потрібно сумістити з площиною рівня, паралельною площині проекцій. У такому положенні плоска фігура проеціюється на відповідну площину проекцій у натуральну величину. Розглянемо спочатку обертання точки О відрізка прямої ОВ навколо горизонталі (рис. 4.14, а). Суть перетворення залишається такою ж, як і у випадку обертання навколо осей, які перпендикулярні до площин проекцій.
а б Рис. 4.14
Під час обертання навколо h точка В описує дугу кола в площині обертання γ. Площина обертання γ перпендикулярна до осі обертання: γ ^ h. Таким чином, γ є горизонтально-проеціюючою площиною: γ ^ П1. Центр обертання – точка О. О = γ Ç h. Радіус обертання точки В (ВО – відрізок прямої загального положення) знаходиться у площині γ. Якщо радіус обертання точки В стане паралельним П1, то він суміститься з площиною рівня, паралельно до П1, в якій знаходиться вісь обертання h. У цій самій площині рівня опиниться і точка В Î R. Способом прямокутного трикутника визначаємо натуральну величину радіуса обертання точки В навколо h. Натуральну величину радіуса обертання відкладаємо від точки В1 на γ1 (або за допомогою циркуля горизонтальну проекцію точки переміщуємо в нове положення В1). В новому положенні точка В знаходиться з горизонталлю h в одній площині, яка паралельна П1. Друга проекція `В2 в цьому випадку буде збігатися з проекцією h – h2. Даний спосіб має обмежене використання. Він корисний, наприклад, якщо потрібно визначити натуральну величину плоскої фігури. Приклад: Визначити натуральну величину DАВС площини загального положення (рис. 4.14, б). Для визначення натуральної величини DАВС, через точки А і l проводимо горизонталь площини. Ці точки при обертанні будуть нерухомими, оскільки вони знаходяться на осі обертання h. Обертатись будуть лише точки В і С. Вони переміщуються по колах у площинах обертання, перпендикулярних до осі обертання h. Для визначення положення точки `В1 після обертання, знаходимо натуральну величину радіуса обертання точки В навколо горизонталі h і цим радіусом переводимо горизонтальну проекцію точки В в нове положення. Аналогічні побудови виконуємо для точки С. Проекція Ā1В1С1 є натуральною величину DАВС, оскільки площина DАВС стала паралельною П1. Фронтальна проекція DАВС збігається з фронтальною проекцією h2 горизонталі, тобто являє собою пряму лінію. Запитання і завдання для самоперевірки 1. Які є способи перетворення креслення та які їх основні відмінності? 2. У чому полягає сутність способу заміни площин проекцій? 3. Укажіть направлення площин проекцій при переведені площини загального положення у горизонтально-проецююче. 4. Укажіть алгоритм розв’язку задачі на визначення справжньої величини площини загального положення способом заміни площин проекцій. 5. У чому полягає сутність способу обертання навколо проеціювальної прямої? 6. Яку пряму приймають за вісь обертання при переведенні площини загального положення у горизонтально-проецююче? 7. Яку пряму приймають за вісь обертання при переведенні площини загального положення у фронтально-проецююче? 8. У чому сутність способу плоско-паралельного переміщення? Які перетворення необхідно здійснити, щоб визначити справжню величину площини загального положення? 9. З якою метою використовується в нарисній геометрії спосіб допоміжного проеціювання? 10. Чи можна за допомогою способів перетворення площин проекцій встановити кут нахилу площини загального положення? 11. Чи можна способом обертання відрізка прямої встановити його довжину і кути нахилу до площин проекцій П1 і П2? Яка з проекцій відрізка прямої лінії не змінює своєї величини?
|