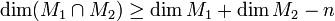Линейным многообразием в линейном пространстве  называется подмножество этого пространства вида
называется подмножество этого пространства вида

для каких-то фиксированных подпространства  и вектора
и вектора  , то есть подмножество, полученное сдвигом каждого элемента из
, то есть подмножество, полученное сдвигом каждого элемента из  на вектор
на вектор  . Обозначение:
. Обозначение:

Если 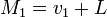 и
и 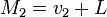 , то
, то 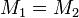 тогда и только тогда, когда и
тогда и только тогда, когда и 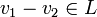 .
.
В частности, 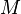 является линейным подпространством тогда и только тогда, когда
является линейным подпространством тогда и только тогда, когда  (т.е.
(т.е. 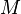 содержит нулевой элемент). В этом случае
содержит нулевой элемент). В этом случае 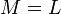 .
.
Если  — гильбертово пространство, а
— гильбертово пространство, а  — его замкнутое подпространство, то можно выбрать вектор
— его замкнутое подпространство, то можно выбрать вектор 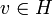 в определении
в определении 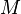 (
(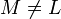 ) ортогональным подпространству
) ортогональным подпространству  . Такое представление
. Такое представление  ,
, 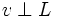 единственно.
единственно.
Пересечение линейных многообразий всегда является линейным многообразием.
Размерность линейного многообразия 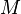 — это размерность линейного подпространства
— это размерность линейного подпространства  :
: 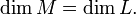 Для линейных многообразий
Для линейных многообразий 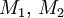 в
в 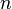 -мерном векторном пространстве или
-мерном векторном пространстве или  , или
, или 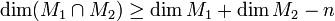

 называется подмножество этого пространства вида
называется подмножество этого пространства вида
 и вектора
и вектора  , то есть подмножество, полученное сдвигом каждого элемента из
, то есть подмножество, полученное сдвигом каждого элемента из 
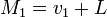 и
и 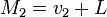 , то
, то 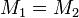 тогда и только тогда, когда и
тогда и только тогда, когда и 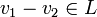 .
.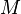 является линейным подпространством тогда и только тогда, когда
является линейным подпространством тогда и только тогда, когда  (т.е.
(т.е. 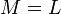 .
.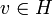 в определении
в определении 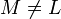 ) ортогональным подпространству
) ортогональным подпространству 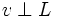 единственно.
единственно.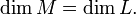 Для линейных многообразий
Для линейных многообразий 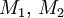 в
в 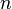 -мерном векторном пространстве или
-мерном векторном пространстве или  , или
, или