Число слагаемых с положительными и отрицательными коэффициентами в каноническом виде квадратичной формы постоянно и не зависит от способа приведения формы к каноническому виду (т.е. от выбора собственного базиса).
Билет 73 положительно (отрицательно) определенные квадратичные формы
Квадратичная форма 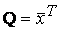 А
А 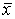 называется:
называется:
1) положительно(отрицательно)-определенной, если для любого ненулевого 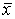 выполняется неравенство
выполняется неравенство 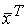 А
А 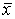 > 0 (
> 0 (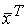 А
А 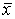 < 0);Ясно, что положительно-определенная квадратичная форма приводится к сумме квадратов с положительными коэффициентами, а положительно-полуопределенная форма – с неотрицательными коэффициентами. Важным условием положительной определенности квадратичной формы является следующий критерий (критерий Сильвестра).Для того чтобы квадратичная форма
< 0);Ясно, что положительно-определенная квадратичная форма приводится к сумме квадратов с положительными коэффициентами, а положительно-полуопределенная форма – с неотрицательными коэффициентами. Важным условием положительной определенности квадратичной формы является следующий критерий (критерий Сильвестра).Для того чтобы квадратичная форма 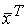 А
А 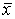 была положительно-определенной, необходимо и достаточно, чтобы были положительны все главные, или угловые, миноры
была положительно-определенной, необходимо и достаточно, чтобы были положительны все главные, или угловые, миноры

матрицы 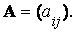 Теперь нетрудно найти и условия отрицательной определенности квадратичной формы. Для того чтобы квадратичная форма
Теперь нетрудно найти и условия отрицательной определенности квадратичной формы. Для того чтобы квадратичная форма 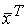 А
А 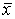 была отрицательно-определенной необходимо и достаточно, чтобы все главные миноры нечетного порядка были отрицательны, а все главные миноры четного порядка – положительны. Теорема. Квадратичная форма
была отрицательно-определенной необходимо и достаточно, чтобы все главные миноры нечетного порядка были отрицательны, а все главные миноры четного порядка – положительны. Теорема. Квадратичная форма 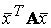 положительно (отрицательно) определена тогда и только тогда, когда все собственные значения матрицы А положительны (отрицательны).
положительно (отрицательно) определена тогда и только тогда, когда все собственные значения матрицы А положительны (отрицательны). 

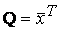 А
А 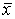 называется:
называется: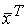 А
А 
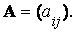 Теперь нетрудно найти и условия отрицательной определенности квадратичной формы. Для того чтобы квадратичная форма
Теперь нетрудно найти и условия отрицательной определенности квадратичной формы. Для того чтобы квадратичная форма 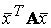 положительно (отрицательно) определена тогда и только тогда, когда все собственные значения матрицы А положительны (отрицательны).
положительно (отрицательно) определена тогда и только тогда, когда все собственные значения матрицы А положительны (отрицательны). 



