ненулевой вектор  называется собственным вектором линейного оператора
называется собственным вектором линейного оператора 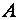 , если существует такое число
, если существует такое число  , что выполняется равенство:
, что выполняется равенство: 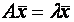 . Число
. Число  называется собственным значением оператора
называется собственным значением оператора 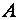 , отвечающим собственному вектору
, отвечающим собственному вектору 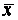 .
.
Множество собственных значений линейного оператора называется его спектром.
Рассмотрим матрицу оператора в некотором базисе:

Тогда соотношение 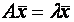 или (
или (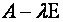 ),
), 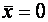 эквивалентно следующему:
эквивалентно следующему:


Это есть однородная система  ого порядка, всегда имеющая нулевое решение
ого порядка, всегда имеющая нулевое решение 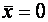 . По правилу Крамера она будет иметь ненулевые решения тогда и только тогда, когда ее определитель равен нулю, т.е.
. По правилу Крамера она будет иметь ненулевые решения тогда и только тогда, когда ее определитель равен нулю, т.е.
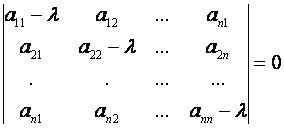 (1)
(1)
Итак, собственные числа  являются корнями алгебраического уравнения
являются корнями алгебраического уравнения  ого порядка (1), которое называется характеристическими уравнением, а его левая часть - характеристическим многочленом.
ого порядка (1), которое называется характеристическими уравнением, а его левая часть - характеристическим многочленом.
Заметим, что собственные значения не зависят от выбора базиса, в котором записывается матрица оператора 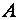 .
.
Пусть  - собственное значение, т.е. решение характеристического уравнения (1). Тогда собственный вектор
- собственное значение, т.е. решение характеристического уравнения (1). Тогда собственный вектор 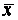 , отвечающий этому собственному значению, будет решением однородной системы
, отвечающий этому собственному значению, будет решением однородной системы
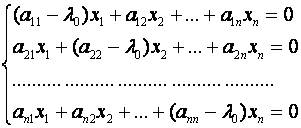 (2)
(2)
Так как множество решений линейной однородной системы является линейным пространством, то для нахождения собственных векторов 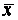 , отвечающих собственному значению
, отвечающих собственному значению  , достаточно найти базис этого пространства.
, достаточно найти базис этого пространства.

 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора 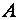 , если существует такое число
, если существует такое число  , что выполняется равенство:
, что выполняется равенство: 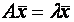 . Число
. Число  называется собственным значением оператора
называется собственным значением оператора 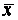 .
.
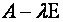 ),
), 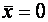 эквивалентно следующему:
эквивалентно следующему:

 ого порядка, всегда имеющая нулевое решение
ого порядка, всегда имеющая нулевое решение  (1)
(1) - собственное значение, т.е. решение характеристического уравнения (1). Тогда собственный вектор
- собственное значение, т.е. решение характеристического уравнения (1). Тогда собственный вектор 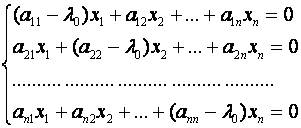 (2)
(2) , достаточно найти базис этого пространства.
, достаточно найти базис этого пространства.


