Билет 68 Ортогональное дополнение
Ортогональным дополнением непустого подмножества Рассмотрим примеры ортогональных дополнений евклидова пространства. 1. Ортогональным дополнением нулевого подпространства 2. Пусть в пространстве 3. В пространстве
Билет 69 Линейные формы Пусть X — линейное пространство. Линейное отображение l: X → R называется линейной формой, или линейной функцией, или линейным функционалом. Это означает, что " x 1, x 2 Î X и " α; Î R l(x 1 + x 2) = l(x 1) + l(x 2), l(αx 1) = α; l(x 1). Теорема 1. Множество линейных форм (функций), заданных на X, является линейным пространством относительно операций
В качестве нулевого элемента l = θ выбирается линейная функция l(x) такая, что " x Î X l(x) = 0. Это пространство называется сопряженным к X и обозначается X *. Теорема 2. Размерности пространств X и X * равны. Пусть e 1, e 2, …, en — базис в Xn. Матрицей линейной формы называется матрица–строка
Обозначим l i = l(ei) коэффициенты (компоненты) линейной формы l(x) в базисе e 1, e 2, …, en. Тогда
Преобразование коэффициентов линейной формы при переходе к новому базису. Пусть даны два базиса e 1, e 2, …, en и f 1, f 2, …, fn, связанные матрицей перехода C = (cik) по формуле f = e · C Þ l' = C · l. Отметим, что коэффициенты линейной формы преобразуются так же, как базисные векторы — посредством матрицы C. В то время как координаты векторов преобразуются посредством матрицы C − 1. Ядро линейной формы (линейного функционала) — линейное пространство. Оно называется гиперплоскостью. Билет 70 Билинейные формы Пусть X — линейное пространство.Функция b (x, y), осуществляющая отображение X × X → R, называется билинейной формой, если она линейна по каждому аргументу, т.е. " x, y, z Î X и " α;, β; Î R
Билинейная форма называется симметричной, если " x, y Î X b (x, y) = b (y, x).Пусть e 1, e 2, …, en — базис в Xn. Тогда " x, y Î Xn
Обозначим bij = b (ei, ej). Воспользовавшись линейностью b (x, y) по обоим аргументам, получим:
Квадратная матрица n –го порядка B = (bij) называется матрицей билинейной формы. Обозначив X и Y координатные столбцы векторов x и y, билинейную форму можно записать в виде:
|

 евклидова пространства
евклидова пространства 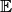 называется множество векторов, ортогональных каждому вектору из
называется множество векторов, ортогональных каждому вектору из 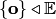 служит все пространство
служит все пространство 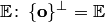 . Ортогональным дополнением всего пространства является его нулевое подпространство
. Ортогональным дополнением всего пространства является его нулевое подпространство 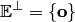 .
.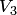 радиус-векторов (с началом в точке
радиус-векторов (с началом в точке  ) за даны три взаимно перпендикулярных радиус-вектора
) за даны три взаимно перпендикулярных радиус-вектора  ,
, 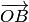 и
и  . Тогда ортогональным дополнением вектора
. Тогда ортогональным дополнением вектора 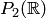 многочленов степени не выше второй со скалярным произведением (8.29) задано подмножество
многочленов степени не выше второй со скалярным произведением (8.29) задано подмножество  - многочленов нулевой степени. Найдем ортогональное дополнение этого подмножества. Для этого приравняем нулю скалярное произведение многочлена
- многочленов нулевой степени. Найдем ортогональное дополнение этого подмножества. Для этого приравняем нулю скалярное произведение многочлена 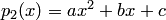 на постоянный многочлен
на постоянный многочлен 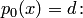
 . Поскольку величина
. Поскольку величина 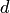 произвольная, то
произвольная, то 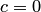 . Следовательно, ортогональным дополнением подмножества
. Следовательно, ортогональным дополнением подмножества 


