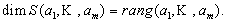Билет 61 Линейная оболочка
Определение 2. Линейной оболочкой системы элементов Непосредственно из определения следует, что любая линейная оболочка является линейным пространством, а любое линейное пространство – линейной оболочкой натянутой на какой-либо базис этого пространства. Теорема 1 (основное свойство линейных оболочек). Любой вектор системы {Пусть, для определенности, Следствие. Размерность линейной оболочки равна рангу соответствующей системы элементов: Билет 62 Способы задания линейных подпространств
|
, принадлежащих L, называется совокупность всех линейных комбинаций этих элементов: 
.
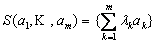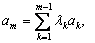а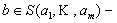 
произвольный. Тогда
, т.е.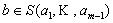 
}
