Билет 58 БазисОпределение 1. Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям: 1) система 2) Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов Примеры. Базис на плоскости (V2 – 2 неколлинеарных вектора), в пространстве (V3 – 3 некомпланарных вектора), в пространстве Rn (канонический базис), в пространстве многочленов степени ≤ n - (1,х,х2,…,хn). Теорема 1. Коэффициенты разложения по базису – единственны. {Пусть Определение 2. Координатами элемента линейного пространства в некотором базисе называются коэффициенты разложения по этому базису. (В силу т. 1 это определение – корректно) Будем писать: В дальнейшем, по умолчанию, будем считать вектор вектором – столбцом, в противном случае будем писать строку координат в явном виде: Теорема 2. При сложении векторов их координаты складываются: { Теорема 3. При умножении вектора на число его координаты умножаются на это число: λа = (λα1,…,λαn). {
|
линейно независима.
): 
}
.
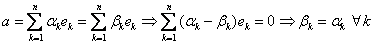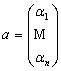либо как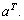 
}
}
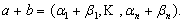
