Билет 67 Евклидово пространство. Ортагональные и ортонормированне системы векторов.
Линейное пространство E = {f, g, h, …} называется евклидовым, если ставится в соответствие число, называемое скалярным произведением: Имеет место Неравенство Коши – Буняковского – Шварца: { По определению, длиной элемента называется: Отсюда легко получить, что в соответствие число Свойство (3) называется неравенством треугольника, а норма есть обобщение понятия ‘длина’. {Предположим, система линейно зависима: Определение 2. Система векторов евклидова пространства { Из теоремы 1 сразу следует, что ортонормированная система элементов всегда линейно независима. Отсюда, в свою очередь, следует, что в n – мерном евклидовом пространстве ортонормированная система из n векторов образует базис (например, { i, j, k } в 3 х – мерном пространстве).Такая система называется ортонормированным базисом, а ее векторы – базисными ортами. Координаты вектора в ортонормированном базисе можно легко вычислить с помощью скалярного произведения: если
|

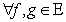
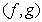 . При этом, для
. При этом, для 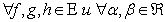 выполняются аксиомы:
выполняются аксиомы:
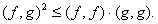
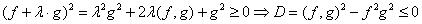 }
} , а косинусом угла между двумя элементами:
, а косинусом угла между двумя элементами:  (В силу неравенства К – Б – Ш это определение корректно)
(В силу неравенства К – Б – Ш это определение корректно) Линейное пространство N называется нормированным, если
Линейное пространство N называется нормированным, если  N ставится
N ставится , называемое нормой элемента
, называемое нормой элемента 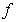 , иудовлетворяющее условиям:
, иудовлетворяющее условиям: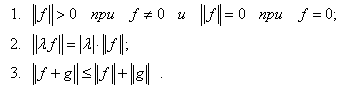
 оп ределение 1. Система векторов евклидова пространства {
оп ределение 1. Система векторов евклидова пространства {  } называется ортогональной, если все ее элементы попарно ортогональны:
} называется ортогональной, если все ее элементы попарно ортогональны: 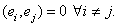 Теорема 1. Ортогональная система неравных нулю векторов линейно независима.
Теорема 1. Ортогональная система неравных нулю векторов линейно независима. и, для определенности,
и, для определенности,  Умножим скалярно равенство на
Умножим скалярно равенство на 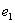 . Учитывая ортогональность системы, получим:
. Учитывая ортогональность системы, получим: 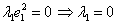 }
}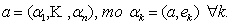 Действительно, умножая равенство
Действительно, умножая равенство 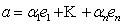 на
на  , получаем указанную формулу.
, получаем указанную формулу.


