Линейные операторы в нормированных пространствахПусть Определение. Оператор
· Если Теорема. Ограниченность оператора эквивалентна каждому из этих свойств: 1. Оператор 2. Оператор переводит единичную сферу Определение. Нормой линеного оператора
Теорема. Линейный оператор непрерывен тогда и только тогда, когда он ограничен.
|
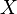и 
- нормированные пространства.
называется непрерывным в точке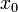 
, если для 
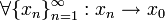справедливо: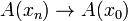 
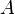- линейный оператор и 
, то 
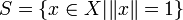в ограниченную сферу.
