Разложение по формуле Маклорена некоторых элементарных функций
Следует отметить, что при разложении функции в ряд применение формулы Маклорена предпочтительнее, чем применение непосредственно формулы Тейлора, т.к. вычисление значений производных в нуле проще, чем в какой-либо другой точке, естественно, при условии, что эти производные существуют. Применение формулы Тейлора для разложения функций в степенной ряд широко используется и имеет огромное значение при проведении различных математических расчетов. Непосредственное вычисление интегралов некоторых функций может быть сопряжено со значительными трудностями, а замена функции степенным рядом позволяет значительно упростить задачу. Нахождение значений тригонометрических, обратных тригонометрических, логарифмических функций также может быть сведено к нахождению значений соответствующих многочленов. Если при разложении в ряд взять достаточное количество слагаемых, то значение функции может быть найдено с любой заданной точностью. Практически можно сказать, что для нахождения значения любой функции с разумной степенью точности (предполагается, что точность, превышающая 10-20 знаков после десятичной точки, необходима очень редко) достаточно 4-10 членов разложения в ряд. Применение принципа разложения в ряд позволяет производить вычисления на ЭВМ в режиме реального времени, что немаловажно при решении конкретных технических задач. Функция f (x) = e x. Находим: f (x) = e x, f (0) = 1, f ¢(x) = e x, f ¢(0) = 1,…, f ( n )(x) = e x, f ( n )(0) = 1.
Пример: Найдем значение числа е. В полученной выше формуле положим х = 1.
Для 8 членов разложения: e = 2,71827876984127003. Для 10 членов разложения: e = 2,71828180114638451 Для 100 членов разложения: e = 2,71828182845904553 Как видно, для достижения точности, достаточной для решения большинства практических задач, можно ограничиться 6-7 – ю членами ряда. Функция f (x) = sin x. Получаем f (x) = sin x; f (0) = 0, f ¢(x) = cos x = sin(x + p/2); f ¢(0) = 1; f ¢¢(x) = –sin x = sin(x + 2p/2); f ¢¢(0) = 0; f ¢¢¢(x) = –cos x = sin(x + 3p/2); f ¢¢¢(0)=–1; ………………………………………… f ( n )(x) = sin(x + p n /2); f ( n )(0) = sin(p n /2); f ( n +1)(x) = sin(x + (n + 1)p/2); f ( n +1)(
Функция f (x) = cos x. Для функции cos x, применив аналогичные преобразования, получим:
Функция f (x) = (1 + x)a (a - действительное число).
Если в полученной формуле принять a = n, где n – натуральное число и f ( n +1)(x)=0, то Rn +1 = 0, тогда
Получилась формула, известная как бином Ньютона. Функция f (x) = ln(1 + x). Получаем: f (x) = ln(1 + x); f (0) = 0; f¢;(x) =
Таким образом:
Полученная формула позволяет находить значения любых логарифмов (не только натуральных) с любой степенью точности. Разложение различных функций по формулам Тейлора и Маклорена приводится в специальных таблицах, однако, формула Тейлора настолько удобна, что для подавляющего большинства функций разложение может быть легко найдено непосредственно. В дальнейшем будут рассмотрены различные применения формулы Тейлора не только к приближенным представлениям функций, но и к решению дифференциальных уравнений и к вычислению интегралов.
|

 Тогда:
Тогда: 
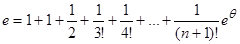
 ) = sin(
) = sin(
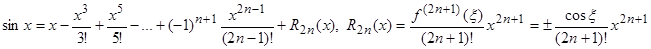


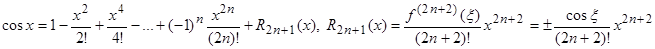
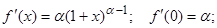
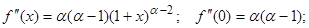 ……….
……….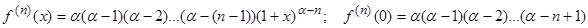
 Тогда:
Тогда:



 ;
; 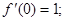
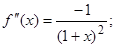
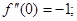

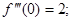




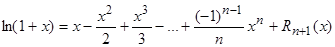 ,
, 



