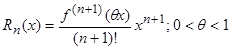ФОРМУЛА ТЕЙЛОРА
Теорема Тейлора. 1) Пусть функция f (x) имеет в точке х = а и некоторой ее окрестности производные порядка (n+1) включительно (т.е. все производные функции до порядка n непрерывны и дифференцируемы в этой окрестности). 2) Пусть х – любое значение из этой окрестности, но х ¹ а. Тогда между точками х и а найдется такая точка
Это выражение называется формулой Тейлора, а выражение: Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т.д. Если в формуле Тейлора положить а = 0, то она запишется в виде
Этот частный случай формулы Тейлора называют формулой Маклорена (Колин Маклорен (1698-1746) шотландский математик)
|
, что справедлива формула:
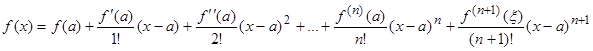
называется остаточным членом в форме Лагранжа.
, 
