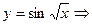Свойства дифференциала.
Если u = f (x) и v = g (x) – функции, дифференцируемые в точке х, то непосредственно из определения дифференциала и таблицы производных следуют следующие свойства: 1) d (u ± v) = (u ± v) ¢dx = u¢dx ± v¢dx = du ± dv. 2) d (uv) = (uv) ¢dx = (u¢v + v¢u) dx = vdu + udv. 3) d (Cu) = Cdu. 4) Дифференциал сложной функции. Инвариантная форма записи дифференциала Найдем выражение для дифференциала сложной функции. Пусть y=f (u), u=g (x) или y = f (g (x)). Тогда по правилу дифференцирования сложной функции: Мы доказали следующую теорему. Теорема. Дифференциал сложной функции y = f (u), для которой u = g (x), имеет тот же вид dy=f '(u) du, какой он имел бы, если бы промежуточный аргумент u был независимой переменной. Иначе говоря, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство дифференциала называется инвариантностью формы дифференциала. Однако, если х – независимая переменная, то dx = D x, но если х зависит от t, то D х ¹ dx. Таким образом, форма записи dy = f ¢(x)D x не является инвариантной. Примеры.
|
.
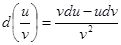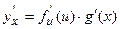. Следовательно, по определению 
, но g '(x) dx = du, поэтому dy= f '(u) du.
