ПРИЗНАКИ ЭКСТРЕМУМА ФУНКЦИИ
Рассмотрим график непрерывной функции y = f (x), изображенной на рисунке. Значение функции в точке x 1 будет больше значений функции во всех соседних точках как слева, так и справа от x 1. В этом случае говорят, что функция имеет в точке x 1 максимум. В точке x 3 функция, очевидно, также имеет максимум. Если рассмотреть точку x 2, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x 2 минимум. Аналогично для точки x 4. Функция y = f (x) в точке x 0 имеет максимум, если существует такая окрестность точки x 0, что для всех x ≠ x 0, принадлежащих этой окрестности, имеет место неравенство f (x) < f (x 0). Функция y = f (x) имеет минимум в точке x 0, если существует такая окрестность точки x 0, что для всех x ≠ x 0, принадлежащих этой окрестности, имеет место неравенство f (x)> f (x0). Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции. Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка. Отметим, что точки экстремума носят локальный характер, т.е. если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке x 1 имеет максимум, хотя есть точки, в которых значения функции больше, чем в точке x 1. В частности, f (x 1) < f (x 4) т.е. минимум функции больше максимума. Из определения максимума следует только, что это самое большое значение функции в точках, достаточно близких к точке максимума. Теорема 1. (Теорема Ферма, Необходимое условие существования экстремума.) Если дифференцируемая функция y = f (x) имеет в точке x= x 0 экстремум, то ее производная в этой точке обращается в нуль. ► Пусть для определенности в точке x 0 функция имеет максимум. Тогда при достаточно малых приращениях Δ x имеем f (x 0+ Δ x) < f (x 0), т.е.
Переходя в этих неравенствах к пределу при Δ x → 0 и учитывая, что производная f '(x 0) существует: Так как f ' (x 0) определяет число, то эти неравенства совместны только в том случае, когда f ' (x 0) = 0.◄ Геометрический смысл теоремы Ферма состоит в том, что если в точке x 0 дифференцируемая функция имеет экстремум, то в точке Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры. Пример. Следствие. Таким образом, из приведенного примера и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует. Обратное утверждение неверно: Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х 3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум. Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются стационарными (лат. стоящий, неподвижный) или критическими точками. Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема. Теорема 2. (I достаточный признак экстремума.) Если непрерывная функция b) минимумом, если знак меняется с минуса на плюс: f ' (x) < 0 при x < x 0 и f ' (x) > 0 при x > x 0. ►По условию, Если f ' (х) > 0 при x < x 0 и и f ' (х) < 0 при x > x 0, то это означает, что слева от точки Аналогично доказывается вторая часть теоремы о минимуме.◄
Исследование функции на экстремум может выполняться и с помощью производных высших порядков. Теорема 3. (II достаточный признак экстремума.) Если функция Если f ¢¢(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование. Максимизация прибыли. Пусть Q – количество реализованного товара, R(Q) – функция дохода, C(Q) – функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организация инфраструктуры и т.п. Прибыль от реализации произведенного товара дается формулой П(Q) = R(Q) – C(Q). В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, необходимо, чтобы предельный доход и придельные издержки были равны. Этот принцип можно записать в виде R '(Q) = C '(Q). Действительно, из необходимого условия экстремума для функции П (Q) следует, что П '(Q) = 0, откуда и получается основной принцип. Пример. Найти максимум прибыли, если доход и издержки определяются следующими формулами: R (Q) = 100 Q – Q 2, C (Q) = Q 3 – 37 Q 2 + 169 Q + 4000. Решение. Прибыль П (Q) = – Q 3 + 36 Q 2 – 69 Q – 4000. Приравнивая производную функцию прибыли к нулю, получаем уравнение Q 2 – 24 Q + 23 = 0. Корни этого уравнения Q 1 = 1, Q 2 = 23. Проверка показывает, что максимальная прибыль достигается при Q = 23; П max =1290.
|

 . Но тогда
. Но тогда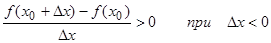

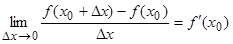 , а следовательно предел, стоящий слева, не зависит от того как Δ x → 0, получаем: при Δ x → – 0 f' (x 0) ≥ 0, а при Δ x → + 0 f' (x 0) ≤ 0.
, а следовательно предел, стоящий слева, не зависит от того как Δ x → 0, получаем: при Δ x → – 0 f' (x 0) ≥ 0, а при Δ x → + 0 f' (x 0) ≤ 0. касательная к графику функции y = f (x) параллельна оси абсцисс. Теорема неверна, если функция рассматривается на отрезке.
касательная к графику функции y = f (x) параллельна оси абсцисс. Теорема неверна, если функция рассматривается на отрезке. y = | x |. Функция не имеет производной в точке x = 0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y (0) = 0, а при всех x ≠ 0 y > 0.
y = | x |. Функция не имеет производной в точке x = 0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y (0) = 0, а при всех x ≠ 0 y > 0.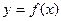 дифференцируема в некоторой окрестности стационарной точки
дифференцируема в некоторой окрестности стационарной точки 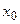 и при переходе через неё (слева направо) производная имеет противоположные знаки, то
и при переходе через неё (слева направо) производная имеет противоположные знаки, то 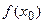 является экстремумом функции, причем: а) максимумом, если знак меняется с плюса на минус: f ' (x) > 0 при x < x 0 и f ' (x) < 0 при x > x 0;
является экстремумом функции, причем: а) максимумом, если знак меняется с плюса на минус: f ' (x) > 0 при x < x 0 и f ' (x) < 0 при x > x 0;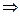 в точке x 0 функция имеет максимум.
в точке x 0 функция имеет максимум. ,
, 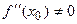 , то в этой точке функция имеет экстремум, причем максимум, если
, то в этой точке функция имеет экстремум, причем максимум, если 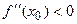 , и минимум, если
, и минимум, если 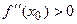 .
.


