ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ. ТОЧКИ ПЕРЕГИБА
График функции На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым. Теорема 1. Пусть
Точка графика непрерывной функции, в которой изменяется выпуклость на вогнутость или наоборот, называется точкой перегиба. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею. Определим достаточные условия того, что данная точка кривой является точкой перегиба. Теорема 2(достаточный признак точки перегиба). Пусть кривая определяется уравнением ►Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0. ◄ Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Заметим, что для непрерывных функций, которые являются дифференцируемыми не во всех точках, также используется понятие выпуклости кривой. Оно возникает, например, в математическом программировании. Здесь не может быть использовано определение, основанное на понятии касательной (касательной в этом случае может и не быть). Поэтому пользуются другим определением, основанным на понятии хорды. График функции (или сама функция) называется выпуклым (выпуклой), если каждая дуга кривой лежит не выше своей хорды. График функции (или сама функция) называется вогнутым (вогнутой), если каждая дуга кривой лежит не ниже своей хорды. В случае дифференцируемых функций определения, основанные на понятиях касательной и хорды, совпадают.
|

 График функции
График функции 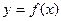 называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.


