ПРАВИЛО ЛОПИТАЛЯ
Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞. Сейчас рассмотрим новое правило раскрытия этих неопределенностей. Теорема (правило Лопиталя). Пусть функции f (x) и g (x) определены и дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a; g¢(x) ≠ 0 в этой окрестности и пусть Коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных. Замечание. Формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует. Например, найти Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности0/0 или ∞/∞, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
|
или 
. Тогда предел отношения функций при х® а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует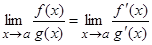 
(1)
. Этот предел существует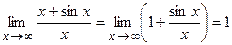 
. Но отношение производных (1 + cos x) / 1 = 1 + cos x при x → ∞ не стремится ни к какому пределу.
