На дом № 3902, 3904, 3906, 3914, 3916, 3936, 3938, 3946.
Дифференциальным уравнением (ДУ) называется уравнение, которое помимо неизвестных функций содержит их производные (или дифференциалы). Если неизвестные функции, входящие в ДУ, зависят только от одной независимой переменной, то ДУ называется обыкновенным ДУ (ОДУ). Уравнение
где Число n называется порядком уравнения (1.1). Функция График решения дифференциального уравнения называется интегральной кривой этого уравнения. Дифференциальное уравнение вида
где Задачей Коши называют задачу нахождения решения
Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку Общим решением дифференциального уравнения (1.2) называется функция 1) функция 2) для любого частного решения Общее решение дифференциального уравнения определяет в некоторой области плоскости XOY семейство интегральных кривых, зависящих от произвольной постоянной С. Частному решению соответствует фиксированная интегральная кривая из этого семейства. Пример 1.1. Проверить, что функция Решение. Функция Полагая Дифференциальное уравнение вида
называется уравнением с разделенными переменными. Уравнение вида:
называется уравнением с разделяющимися переменными. Делением на произведение
Замечание. Деление на произведение Рассмотрим примеры.
3901. Найти общее решение уравнения:
Решение. Преобразуем уравнение:
Чтобы разделить переменные в уравнении, умножим его на выражение После алгебраических преобразований получим:
Проинтегрировав, получим:
После потенцирования: Далее, при делении на скобку
3903. Найти общее решение уравнения:
Решение. Запишем уравнение в таком виде:
Интегрируя, получим общее решение уравнения:
3913. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям:
Решение. Проведем разделение переменных и несложные тригонометрические преобразования:
После интегрирования получим:
Далее, потенцируем
и подставляем начальные условия:
Ответ: Дифференциальное уравнение
Вводя новую неизвестную функцию
Пример 1.2. Решение. Пусть
Разделим переменные и проинтегрируем:
а так как
После обратной замены переменных
При разделении переменных имело место деление на выражение
3937. Решить уравнение Это – однородное уравнение. Замена переменных
(В числителе первого интеграла прибавили и вычли
Возвращаясь к старым переменным, получим ответ:
Контрольные вопросы.
|

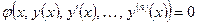 , (1.1)
, (1.1)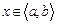 называется обыкновенным дифференциальным уравнением относительно функции
называется обыкновенным дифференциальным уравнением относительно функции 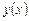 на промежутке
на промежутке 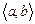 .
. называется частным решением ОДУ (1.1), если после замены
называется частным решением ОДУ (1.1), если после замены 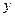 на
на 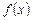 ,
, 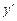 на
на  ,...,
,..., 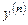 на
на  уравнение обращается в тождество на промежутке
уравнение обращается в тождество на промежутке  . (Предполагается, что
. (Предполагается, что 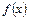 - достаточно гладкая функция.)
- достаточно гладкая функция.) , (1.2)
, (1.2)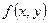 определена в области D на плоскости XOY, называется ОДУ первого порядка, разрешенным относительно производной.
определена в области D на плоскости XOY, называется ОДУ первого порядка, разрешенным относительно производной.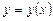 уравнения (1.2), удовлетворяющего начальному условию
уравнения (1.2), удовлетворяющего начальному условию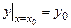 , где
, где 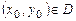 .
.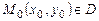 .
.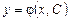 , зависящая от одной произвольной постоянной С, если
, зависящая от одной произвольной постоянной С, если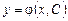 удовлетворяет дифференциальному уравнению при любых допустимых значениях С;
удовлетворяет дифференциальному уравнению при любых допустимых значениях С;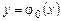 уравнения (1.2) можно подобрать постоянную C, такую, что
уравнения (1.2) можно подобрать постоянную C, такую, что 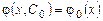
 на
на 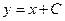 есть общее решение дифференциального уравнения
есть общее решение дифференциального уравнения 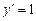 и найти частное решение, удовлетворяющее начальному условию
и найти частное решение, удовлетворяющее начальному условию 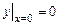 . Дать геометрическое истолкование результата.
. Дать геометрическое истолкование результата.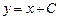 удовлетворяет данному дифференциальному уравнению при любых значениях постоянной С, так как
удовлетворяет данному дифференциальному уравнению при любых значениях постоянной С, так как  .
.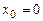 и
и 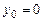 , получим частное решение
, получим частное решение 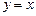 при
при  . Общее решение
. Общее решение 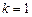 , частное решение
, частное решение 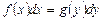

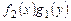 оно приводится к уравнению с разделенными переменными
оно приводится к уравнению с разделенными переменными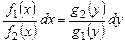 .
. может привести к потере частных решений, обращающих в нуль произведение
может привести к потере частных решений, обращающих в нуль произведение 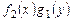 .
.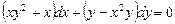 .
.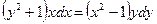 .
.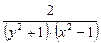 .
.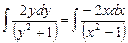 или
или 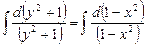 .
.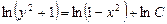 .
. ,
, 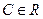 .
.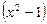 могли быть потеряны решения
могли быть потеряны решения  и
и 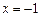 . Подстановка их в дифференциальное уравнение обращает его в тождество. Следовательно, это тоже решения.
. Подстановка их в дифференциальное уравнение обращает его в тождество. Следовательно, это тоже решения.
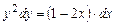 .
.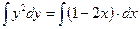 ,
,  ,
,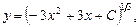
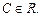
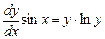 ;
; 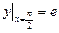 .
.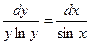
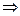
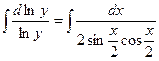
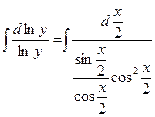
 .
.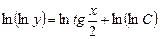 .
.
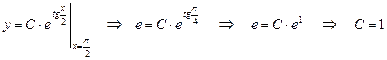 .
.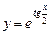 .
. .
.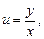 имеем
имеем 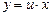 ,
, 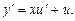 После подстановки получаем уравнение с разделяющимися переменными:
После подстановки получаем уравнение с разделяющимися переменными: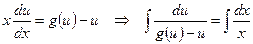 .
.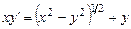 .
.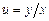 , или
, или  , Тогда
, Тогда  и
и 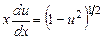 .
.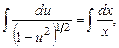
 или
или  ,
, , то, обозначая
, то, обозначая 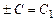 , получаем
, получаем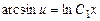 , где
, где 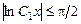 .
. или
или 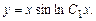
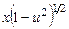 , что могло привести к потере решений, обращающих в нуль это выражение. Здесь
, что могло привести к потере решений, обращающих в нуль это выражение. Здесь 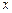 - независимая переменная, а из
- независимая переменная, а из 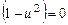 следует
следует 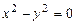 , откуда
, откуда 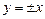 . Проверкой убеждаемся, что функции
. Проверкой убеждаемся, что функции 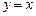 и
и  также являются решениями дифференциального уравнения, поэтому общее решение:
также являются решениями дифференциального уравнения, поэтому общее решение: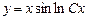 ,
, 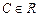 .
.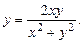
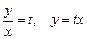 ,
, 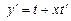 позволит разделить переменные:
позволит разделить переменные:
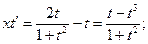
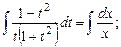

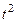 и разделили почленно.) После интегрирования имеем:
и разделили почленно.) После интегрирования имеем: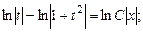

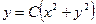 ,
, 


