Пусть дано дифференциальное уравнение:
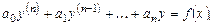
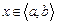 (6.9)
(6.9)
с постоянными коэффициентами 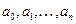 и
и 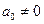 .
.
Теорема. Общее решение неоднородного уравнения (6.9) равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения.
Отыскание общего решения соответствующего однородного уравнения осуществляется по правилам, изложенным выше. Частное решение неоднородного уравнения для случая правых частей специального вида находится методом подбора, или иначе, методом неопределенных коэффициентов.
Общий вид правой части уравнения (6.9), при котором применим метод неопределенных коэффициентов, следующий:
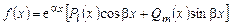 . (6.10)
. (6.10)
Здесь 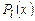 и
и 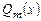 – многочлены степени l и m соответственно. В этом случае частное решение уравнения (6.9) ищем в следующем виде:
– многочлены степени l и m соответственно. В этом случае частное решение уравнения (6.9) ищем в следующем виде:
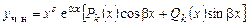 , (6.11)
, (6.11)
где 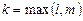 ,
, 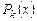 и
и 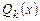 – многочлены от
– многочлены от  степени k общего вида с неопределенными коэффициентами, а
степени k общего вида с неопределенными коэффициентами, а 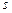 – кратность корня
– кратность корня 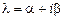
 характеристического уравнения. (Если
характеристического уравнения. (Если 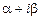 не является корнем, то
не является корнем, то 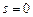 .)
.)
Пример 6.4. Решение уравнения 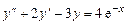 .
.
Решение. Сначала найдем общее решение соответствующего однородного уравнения
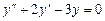 .
.
Его характеристическое уравнение:
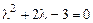
имеет корни 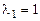 и
и 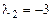 . Общее решение однородного уравнения:
. Общее решение однородного уравнения:
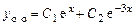 .
.
Теперь нужно найти частное решение неоднородного уравнения. Сравнивая его правую часть с формулой (6.10), видим, что 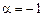 ,
,  . Число
. Число  корнем характеристического уравнения не является, следовательно,
корнем характеристического уравнения не является, следовательно, 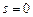 . P и Q – многочлены нулевой степени, следовательно, частное решение будем искать в виде
. P и Q – многочлены нулевой степени, следовательно, частное решение будем искать в виде
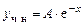 .
.
Удобно расположить 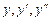 в столбик, написав слева значения коэффициентов из исходного уравнения:
в столбик, написав слева значения коэффициентов из исходного уравнения:
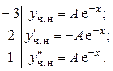
Сложив всё, получим:
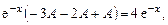
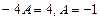 ,
,
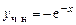 ,
,
а общее решение неоднородного уравнения
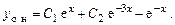
Пример 6.5. Решить уравнение
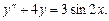
Решение. Однородное уравнение имеет вид
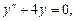
его характеристическое уравнение:
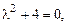 корни
корни 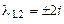 .
.
Общее решение:
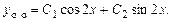
Чтобы правильно выбрать вид частного решения неоднородного уравнения согласно формуле (6.11), сравним правую часть уравнения с общим её представлением по формуле (6.10). Очевидно, 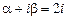 является однократным корнем характеристического уравнения, поэтому
является однократным корнем характеристического уравнения, поэтому 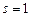 . (В физике это явление называется резонансом, суть его в совпадении собственной частоты колеблющейся системы и частоты приложенной внешней силы.) Кроме того, замечаем, что степени многочленов P и Q – нулевые. Вид частного решения:
. (В физике это явление называется резонансом, суть его в совпадении собственной частоты колеблющейся системы и частоты приложенной внешней силы.) Кроме того, замечаем, что степени многочленов P и Q – нулевые. Вид частного решения:
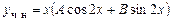 .
.
Подставим в исходное уравнение:

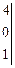
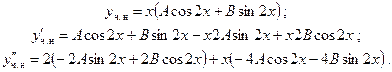
В итоге
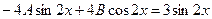 ;
;
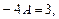

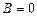 ,
, 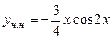 .
.
Общее решение:
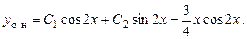
4275 (1-6). Решить уравнение
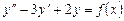 ,
,
где 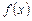 равна:
равна:
1) 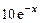 , 2)
, 2) 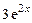 , 3)
, 3) 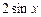 , 4)
, 4) 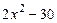 , 5)
, 5) 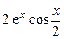 , 6)
, 6) 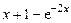 .
.
1. 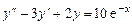 .
.
Решение. Характеристическое уравнение 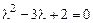 , его корни
, его корни 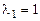 ,
, 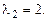 Общее решение однородного уравнения:
Общее решение однородного уравнения:
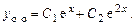
Частное решение неоднородного уравнения ищем в виде 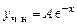 , так как из сопоставления правой части уравнения с формулой (6.10) очевидно, что
, так как из сопоставления правой части уравнения с формулой (6.10) очевидно, что 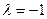 не является корнем характеристического уравнения, т.е. резонанса нет. Подставив
не является корнем характеристического уравнения, т.е. резонанса нет. Подставив 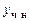 в исходное уравнение, получим
в исходное уравнение, получим
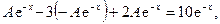
откуда
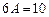 ,
, 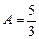 .
.
Общее решение неоднородного уравнения:
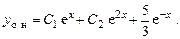
2. 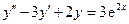 .
.
Решение. Правая часть уравнения имеет вид 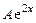 ,
, 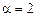 ,
, 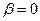 , следовательно,
, следовательно, 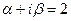 совпадает с однократным корнем характеристического уравнения,
совпадает с однократным корнем характеристического уравнения, 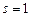 , поэтому вид частного решения неоднородного уравнения
, поэтому вид частного решения неоднородного уравнения 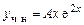 . Найдем А:
. Найдем А:
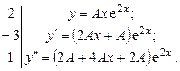
После сложения получим
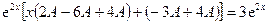 ,
, 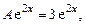
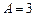 .
.
Общее решение неоднородного уравнения:
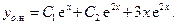
3. 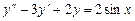 .
.
Решение. Правая часть уравнения имеет вид 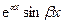 ,
, 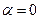 ,
, 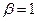 , Корни характеристического уравнения не совпадают с числом
, Корни характеристического уравнения не совпадают с числом 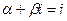 , следовательно резонанса нет и частное решение имеет вид:
, следовательно резонанса нет и частное решение имеет вид:
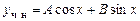 .
.
Подставив в уравнение, получим
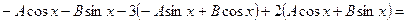
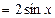 .
.
Приравняв коэффициенты при 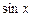 и
и 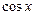 в левой и правой частях равенства, имеем:
в левой и правой частях равенства, имеем:
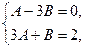 откуда
откуда 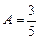 ,
, 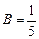 .
.
В итоге общее решение уравнения:
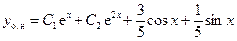 .
.
4. 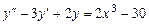 .
.
Решение. Частное решение ищем в виде многочлена с неопределенными коэффициентами, степень которого совпадает со степенью многочлена в правой части уравнения:
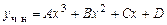 .
.
После подстановки в уравнение получаем
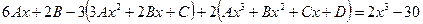 .
.
Приравняв коэффициенты при 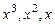 и 1 слева и справа, имеем:
и 1 слева и справа, имеем:
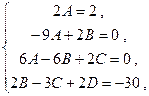
откуда
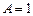 ,
, 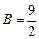 ,
, 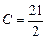 ,
, 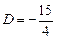 .
.
Общее решение уравнения

Контрольные вопросы.
- Запишите общий вид линейного дифференциального уравнения
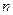 -го порядка.
-го порядка. - В каком случае линейное дифференциальное уравнение называется однородным (ЛОДУ), а в каком – неоднородным (ЛНДУ)?
- Сформулируйте определения линейно зависимой и линейно независимой системы функций на отрезке.
- Сформулируйте определение фундаментальной системы решений ЛОДУ. Как строится общее решение ЛОДУ?
- Что такое определитель Вронского системы функций?
- Как составляется характеристическое уравнение для данного ЛОДУ?
- Выпишите вид ФСР и общего решения ЛОДУ в случаях, если корни характеристического уравнения: а) действительные и различные; б) действительные, но среди них есть кратные; в) комплексные различные; г) комплексные кратные.
- Опишите метод неопределенных коэффициентов решения ЛНДУ со специальным видом правой части (неоднородности).

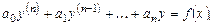
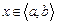 (6.9)
(6.9)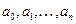 и
и 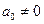 .
.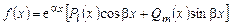 . (6.10)
. (6.10)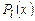 и
и 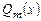 – многочлены степени l и m соответственно. В этом случае частное решение уравнения (6.9) ищем в следующем виде:
– многочлены степени l и m соответственно. В этом случае частное решение уравнения (6.9) ищем в следующем виде: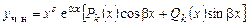 , (6.11)
, (6.11)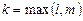 ,
, 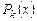 и
и 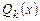 – многочлены от
– многочлены от  степени k общего вида с неопределенными коэффициентами, а
степени k общего вида с неопределенными коэффициентами, а 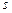 – кратность корня
– кратность корня 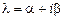
 характеристического уравнения. (Если
характеристического уравнения. (Если 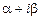 не является корнем, то
не является корнем, то 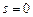 .)
.)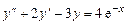 .
.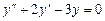 .
.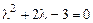
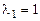 и
и 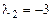 . Общее решение однородного уравнения:
. Общее решение однородного уравнения: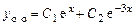 .
.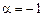 ,
, 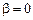 . Число
. Число 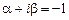 корнем характеристического уравнения не является, следовательно,
корнем характеристического уравнения не является, следовательно, 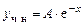 .
.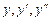 в столбик, написав слева значения коэффициентов из исходного уравнения:
в столбик, написав слева значения коэффициентов из исходного уравнения: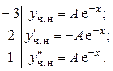
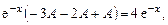
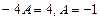 ,
,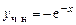 ,
,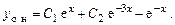
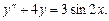
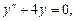
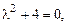 корни
корни 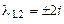 .
.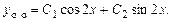
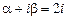 является однократным корнем характеристического уравнения, поэтому
является однократным корнем характеристического уравнения, поэтому 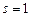 . (В физике это явление называется резонансом, суть его в совпадении собственной частоты колеблющейся системы и частоты приложенной внешней силы.) Кроме того, замечаем, что степени многочленов P и Q – нулевые. Вид частного решения:
. (В физике это явление называется резонансом, суть его в совпадении собственной частоты колеблющейся системы и частоты приложенной внешней силы.) Кроме того, замечаем, что степени многочленов P и Q – нулевые. Вид частного решения: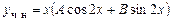 .
.
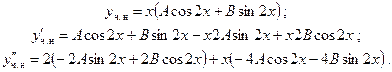
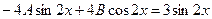 ;
;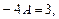

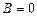 ,
, 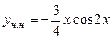 .
.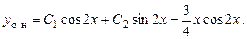
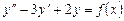 ,
,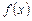 равна:
равна: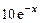 , 2)
, 2) 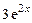 , 3)
, 3) 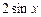 , 4)
, 4) 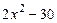 , 5)
, 5) 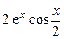 , 6)
, 6) 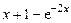 .
.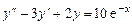 .
.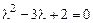 , его корни
, его корни 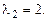 Общее решение однородного уравнения:
Общее решение однородного уравнения: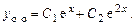
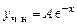 , так как из сопоставления правой части уравнения с формулой (6.10) очевидно, что
, так как из сопоставления правой части уравнения с формулой (6.10) очевидно, что 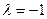 не является корнем характеристического уравнения, т.е. резонанса нет. Подставив
не является корнем характеристического уравнения, т.е. резонанса нет. Подставив 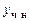 в исходное уравнение, получим
в исходное уравнение, получим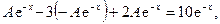
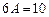 ,
, 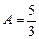 .
.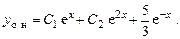
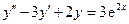 .
.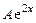 ,
, 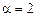 ,
, 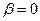 , следовательно,
, следовательно, 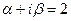 совпадает с однократным корнем характеристического уравнения,
совпадает с однократным корнем характеристического уравнения, 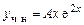 . Найдем А:
. Найдем А: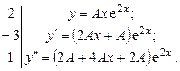
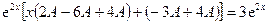 ,
, 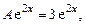
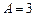 .
.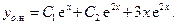
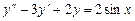 .
.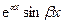 ,
, 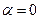 ,
, 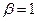 , Корни характеристического уравнения не совпадают с числом
, Корни характеристического уравнения не совпадают с числом 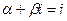 , следовательно резонанса нет и частное решение имеет вид:
, следовательно резонанса нет и частное решение имеет вид: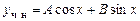 .
.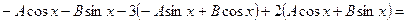
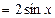 .
.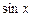 и
и 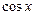 в левой и правой частях равенства, имеем:
в левой и правой частях равенства, имеем: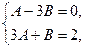 откуда
откуда 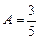 ,
, 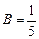 .
.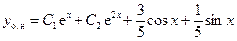 .
.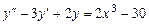 .
.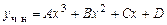 .
.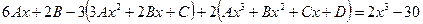 .
.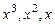 и 1 слева и справа, имеем:
и 1 слева и справа, имеем: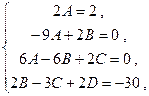
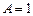 ,
, 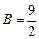 ,
, 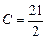 ,
, 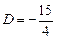 .
.
 -го порядка.
-го порядка.


