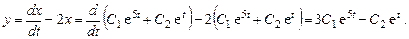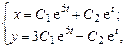На дом №4324.2, 4324.3, 4324.4, 4326, 4331.
Система обыкновенных дифференциальных уравнений первого порядка вида
где Число n называется порядком нормальной системы (7.1). Две системы дифференциальных уравнений называются эквивалентными, если они обладают одними и теми же решениями. Частным решением системы на интервале
определенных и непрерывно дифференцируемых в интервале Нормальная система n уравнений первого порядка
сводится к одному уравнению прядка Метод исключения состоит в следующем. Из уравнений системы и уравнений, получающихся дифференцированием уравнений системы, исключаем все неизвестные функции, кроме одной. Для неё получаем одно ОДУ более высокого порядка. Решая полученное уравнение, определяем одну из функций, а остальные находим без интегрирования, из исходных уравнений и их следствий. Проиллюстрируем этот метод на примере системы второго порядка.
Здесь
Подставив во второе уравнение системы вместо
где Пример 7.1. Решить систему уравнений:
Решение. Из первого уравнения системы находим
откуда
Подставив это во второе уравнение системы (7.4), получим линейное уравнение с постоянными коэффициентами второго порядка
Его общее решение находим изученными ранее методами:
Подставив его производную в выражение для
4324.2. Решить систему уравнений:
Решение ищем методом исключения, преобразуя систему в уравнение второго порядка. Выразим
или
Характеристическое уравнение:
Общее решение:
Подставив найденное
Общее решение системы:
Контрольные вопросы.
|

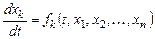 ,
, 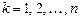 , (7.1)
, (7.1) – независимая переменная;
– независимая переменная;  – неизвестные функции переменной
– неизвестные функции переменной 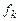 определены в некоторой области D переменных
определены в некоторой области D переменных 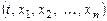 .
. называется совокупность любых n функций
называется совокупность любых n функций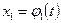 ,
,  ,
, 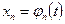 ,
,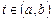 .
.
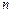 . На этом основан один из методов интегрирования систем дифференциальных уравнений – метод исключения.
. На этом основан один из методов интегрирования систем дифференциальных уравнений – метод исключения. (7.2)
(7.2) – постоянные;
– постоянные; 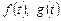 – заданные функции;
– заданные функции; 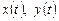 – искомые функции. Из первого уравнения системы (7.2) находим:
– искомые функции. Из первого уравнения системы (7.2) находим: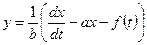 . (7.3)
. (7.3) правую часть выражения (7.3), а вместо
правую часть выражения (7.3), а вместо  – её производную, получим уравнение второго порядка относительно
– её производную, получим уравнение второго порядка относительно 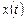 :
: ,
,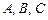 – новые постоянные, связанные с
– новые постоянные, связанные с 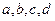 , а
, а  – функция от
– функция от  , полученная из
, полученная из 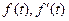 и
и  . Из этого уравнения находим
. Из этого уравнения находим 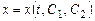 . Подставив
. Подставив  и
и 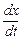 в равенство (7.3), найдем
в равенство (7.3), найдем 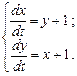 (7.4)
(7.4)
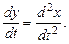
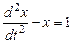 .
.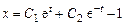 .
.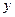 , получаем
, получаем ,
,  .
.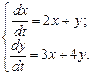
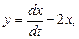
 ,
, .
.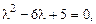 корни
корни 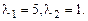
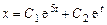 .
. в выражение для
в выражение для