Другие виды уравнений, решаемых методом введения параметра.
А. Уравнение вида
Полагаем
Это общее решение дифференциального уравнения в параметрической форме. Пример 4.2. Решить уравнение
Решение. Положим
откуда
Общее решение будет иметь вид:
В. Уравнение вида
Пример 4.3. Решить уравнение
Решение. Положим
В итоге
4117. Решить уравнение Решение. Это уравнение Клеро. После введения параметра
Взяв полный дифференциал и заменив
Если
Далее, подставив
Очевидно, что (4.11) может быть получено из (4.10) дифференцированием по параметру C, следовательно, в соответствии с изложенным ранее, система уравнений (4.10), (4.11) в параметрической форме описывает особое решение уравнения, графиком которого является огибающая семейства прямых, заданных общим решением (4.10). Исключив параметр C из системы уравнений (4.10), (4.11), найдем уравнение огибающей в явном виде:
Контрольные вопросы.
|
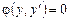разрешимо относительно y:
.
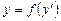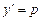, тогда 
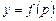. Дифференцируем последнее уравнение и, заменив dy на pdx, получаем 
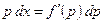, откуда
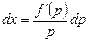и 
, 
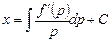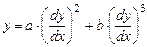(a и b – постоянные).
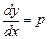, тогда 
,
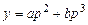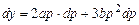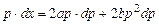или 
,
и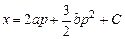 
.
.
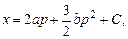
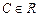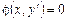разрешимо относительно 
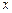, т.е. 
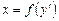. Полагая 
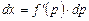. Кроме того, 
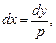т.е. 
и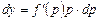 
. Проинтегрировав, найдем общее решение дифференциального уравнения в параметрической форме:
, 
.
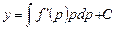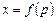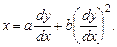
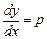, тогда 
,
, 
.
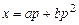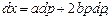
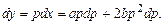
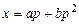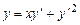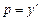уравнение имеет вид:
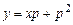. (4.9)
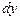на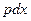 
, получим:
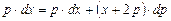, откуда 
.
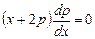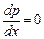, то 
. Подставив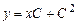 
. (4.10)
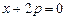, имеем
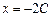. (4.11)
.
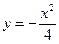