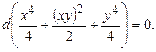На дом. № 4054, 4073, 4059, 4062, 4074.
Дифференциальное уравнение
называется уравнением в полныx дифференциалаx, если его левая часть представляет собой полный дифференциал некоторой функции
Теорема. Пусть функции
непрерывны в односвязной области D плоскости XOY. Выражение
Пример 3.1. Решить уравнение
Решение. Проверим, является ли (3.3) уравнением в полных дифференциалах:
=
следовательно,
= Частную производную
откуда следует:
Общий интеграл уравнения:
При интегрировании некоторых дифференциальных уравнений можно так сгруппировать члены, что получатся легко интегрируемые комбинации. В частности, можно выделять полные дифференциалы, используя известные формулы:
Пример 3.2. Решить уравнение
Решение. Здесь
Тогда
и уравнение (3.4) можно записать в виде:
или
Следовательно,
есть общий интеграл дифференциального уравнения (3.4).
Контрольные вопросы.
|

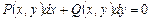 (3.1)
(3.1) , т.е.
, т.е.

 ,
, 

 есть полный дифференциал только тогда, когда выполнено условие
есть полный дифференциал только тогда, когда выполнено условие в D. (3.2)
в D. (3.2) . (3.3)
. (3.3) =
=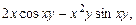

 , т.е. (3.3) – уравнение в полных дифференциалах и
, т.е. (3.3) – уравнение в полных дифференциалах и  , поэтому
, поэтому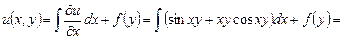
 .
. найденной функции
найденной функции 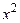 cos xy, что даёт
cos xy, что даёт ,
,  и
и 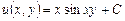 .
. ,
, 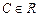 .
. ,
,  ,
,  и т.п.
и т.п.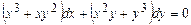 . (3.4)
. (3.4) ,
,  , следовательно, (3.4) – уравнение в полных дифференциалах. Сгруппируем его члены так:
, следовательно, (3.4) – уравнение в полных дифференциалах. Сгруппируем его члены так: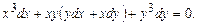
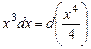 ,
, 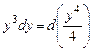 ,
,