На дом. № 4155, 4156, 4159, 4160, 4163, 4169, 4189, 4208.
Дифференциальное уравнение
или, если оно разрешено относительно
Здесь функция
а D – область в Всякая функция Задача нахождения решения
называется задачей Коши для уравнения (5.1) (Здесь Общим решением дифференциального уравнения
будет частным решением уравнения (5.1), удовлетворяющим условиям (5.2). В процессе интегрирования уравнения Рассмотрим три вида дифференциальных уравнений, допускающих понижение порядка. 1. Уравнение вида
Пример 5.1. Решить уравнение Решение. Интегрируя последовательно данное уравнение, имеем:
2. Уравнение, не содержащее искомой функции и её производных до порядка
Порядок уравнения можно понизить на k единиц заменой
Уравнение примет вид:
Из этого уравнения определяем
а затем из уравнения
находим y k -кратным интегрированием.
Пример 5.2. Решить уравнение Решение. Полагая
Последовательно интегрируя, получаем:
3. Уравнение не содержит независимой переменной:
Подстановка
Подстановка этих выражений в уравнение приводит к понижению порядка на единицу.
Пример 5.3. Решить уравнение Решение. Уравнение не содержит независимой переменной x. Полагая
Подстановкой
общее решение которого
После обратной замены
а после разделения переменных
Проинтегрировав, получаем
откуда
Это общий интеграл данного уравнения.
4209. Решить уравнение Решение. Интегрируя уравнение последовательно три раза, получим:
Это и есть общее решение исходного уравнения.
4163. Решить уравнение Решение. Уравнение не содержит искомой функции
откуда
Проинтегрировав, получим
Учтем, что
и
Это есть общее решение.
4171. Решить уравнение Решение. Уравнение не содержит переменной
Подставив всё в уравнение, получим:
После интегрирования:
и наконец,
Контрольные вопросы.
|

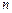 -го порядка имеет вид
-го порядка имеет вид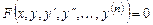 ,
, 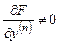 ,
, ,
,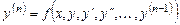 . (5.1)
. (5.1) переменной
переменной 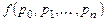 определена в некоторой области
определена в некоторой области 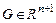 ,
,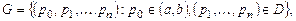
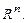
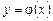 , определенная и
, определенная и 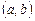 , называется решением этого уравнения, если она обращает его в тождество при подстановке.
, называется решением этого уравнения, если она обращает его в тождество при подстановке.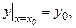

 (5.2)
(5.2)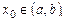
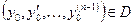 ). Условия (5.2) называются условиями Коши или начальными условиями.
). Условия (5.2) называются условиями Коши или начальными условиями.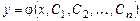 , содержащей n произвольных независимых между собой постоянных
, содержащей n произвольных независимых между собой постоянных 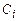 ,
, 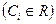 , таких, что, если заданы начальные условия (5.2), то могут быть найдены все значения
, таких, что, если заданы начальные условия (5.2), то могут быть найдены все значения  , при которых
, при которых
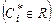
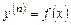 . После
. После 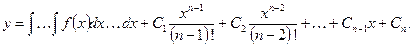
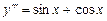 .
.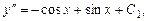

 .
.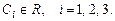
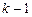 включительно:
включительно: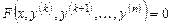 .
.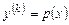 .
. .
. ,
,  ,
,
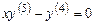 .
.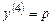 , получаем
, получаем  , откуда
, откуда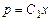 ,
, 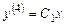 .
.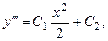
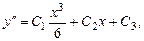
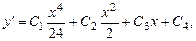
 ,
,
 .
. позволяет понизить прядок уравнения на единицу. Производные
позволяет понизить прядок уравнения на единицу. Производные  выражаются через производные функции
выражаются через производные функции  .
. ,
, 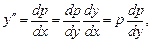
 и т.д.
и т.д.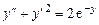 .
.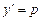 ,
, 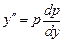 , получаем уравнение
, получаем уравнение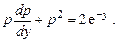
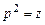 оно сводится к линейному уравнению
оно сводится к линейному уравнению ,
, .
.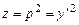 имеем
имеем
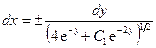 ,
,  .
.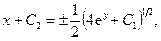
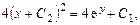
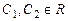 .
.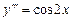 .
. ,
, 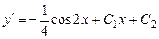 ,
,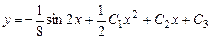 ,
,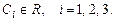
 .
.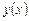 , замена переменной
, замена переменной  позволит понизить порядок уравнения и оно примет вид
позволит понизить порядок уравнения и оно примет вид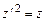 или
или  ,
,
 .
.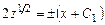 ,
, 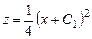 .
.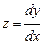 , и продолжим интегрирование:
, и продолжим интегрирование: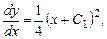

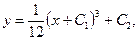
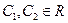 .
.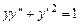 .
.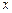 . Будем считать
. Будем считать  независимой переменной, а в качестве искомой функции примем
независимой переменной, а в качестве искомой функции примем , тогда
, тогда 
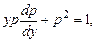 откуда
откуда 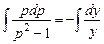 .
.
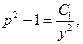

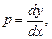

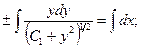
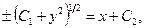

 -го порядка.
-го порядка.


