Ниже приведены формулировки признаков сходимости рядов с неотрицательными членами.
Признак Даламбера. Если для ряда  с неотрицательными членами существует предел
с неотрицательными членами существует предел 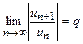 , то этот ряд сходится при
, то этот ряд сходится при 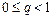 и расходится при
и расходится при 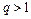 . Случай
. Случай 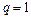 требует дополнительного исследования. При
требует дополнительного исследования. При 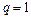 возможны различные случаи. Так, гармонический ряд
возможны различные случаи. Так, гармонический ряд 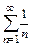 расходится, а ряд
расходится, а ряд  сходится, хотя для обоих этих рядов
сходится, хотя для обоих этих рядов 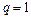 .
.
Признак Коши. Если для ряда  существует предел
существует предел 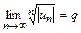 , то этот ряд сходится при
, то этот ряд сходится при 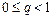 и расходится при
и расходится при 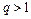 . Случай
. Случай 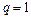 требует дополнительного исследования. Ситуация с
требует дополнительного исследования. Ситуация с 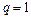 может быть проиллюстрирована теми же примерами, что и в случае признака Даламбера.
может быть проиллюстрирована теми же примерами, что и в случае признака Даламбера.
Интегральный признак Коши. Если 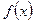 при
при 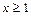 непрерывная, неотрицательная и монотонно убывающая функция, то ряд с неотрицательными членами
непрерывная, неотрицательная и монотонно убывающая функция, то ряд с неотрицательными членами  , где
, где 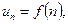 сходится или расходится вместе с несобственным интегралом
сходится или расходится вместе с несобственным интегралом 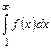 .
.
Пример 11.1. Исследовать на сходимостьряд Дирихле
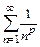 (11.1)
(11.1)
Решение. При 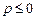 не выполняется необходимый признак сходимости (теорема 9.2), следовательно, ряд расходится. Члены ряда (11.1) являются значениями функции
не выполняется необходимый признак сходимости (теорема 9.2), следовательно, ряд расходится. Члены ряда (11.1) являются значениями функции 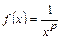 в точках
в точках 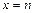 . Функция
. Функция 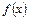 неотрицательна и монотонно убывает (если
неотрицательна и монотонно убывает (если  ) при
) при 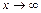 , поэтому ряд (11.1) сходится или расходится вместе с несобственным интегралом
, поэтому ряд (11.1) сходится или расходится вместе с несобственным интегралом 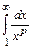 . При
. При  имеем
имеем
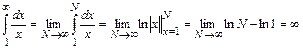 ,
,
а при 
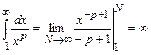 ,
,
следовательно, при 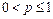 ряд Дирихле расходится. Если же
ряд Дирихле расходится. Если же 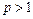 , то
, то
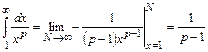 ,
,
следовательно, при 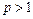 ряд Дирихле сходится.
ряд Дирихле сходится.
Рассмотрим примеры исследования сходимости числовых рядов с помощью сформулированных признаков сходимости. В примерах 11.2, 11.3 и 11.4 используем признак Даламбера.
Пример 11.2. Исследовать на сходимость ряд
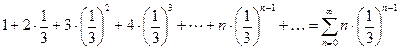 .
.
Решение. Общие члены ряда
 ,
,  .
.
Вычислим предел
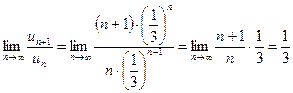 ,
,
следовательно, исследуемый ряд 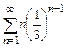 сходится.
сходится.
Пример 11.3. Исследовать на сходимость ряд
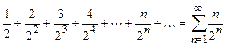 .
.
Решение. Для этого ряда имеем:
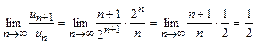 .
.
Следовательно, исследуемый ряд 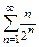 сходится.
сходится.
Пример 11.4. Исследовать на сходимость ряд

Решение. Предел
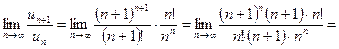
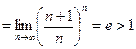 .
.
Следовательно, исследуемый ряд 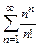 расходится.
расходится.
Исследование ряда в примере 11.5 проведём с помощью признака Коши.
Пример 11.5. Исследовать на сходимость ряд
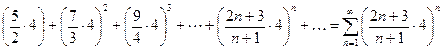 .
.
Решение. Предел
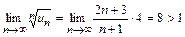 ,
,
следовательно, ряд расходится.
Пример 11.6. С помощью интегрального признака Коши исследовать сходимость ряда
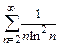 .
.
Решение. Функция 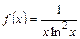 неотрицательна и убывает при
неотрицательна и убывает при 
 , т.е.
, т.е. 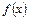 удовлетворяет всем требованиям интегрального признака сходимости Коши. Несобственный интеграл
удовлетворяет всем требованиям интегрального признака сходимости Коши. Несобственный интеграл
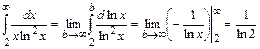
сходится, а вместе с ним сходится и исследуемый ряд.
Определение. Ряд
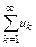 (11.1)
(11.1)
со знакопеременными членами сходится абсолютно, если сходится ряд
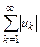 . (11.2)
. (11.2)
Теорема 11.1. Если ряд сходится абсолютно, то он и просто сходится.
Заметим, что абсолютная сходимость ряда – требование более сильное, чем просто сходимость, так как сходимость ряда  не влечёт за собой сходимость ряда
не влечёт за собой сходимость ряда 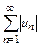 .
.
Для того, чтобы ответить на вопрос, сходится ряд абсолютно или нет, достаточно исследовать сходимость ряда с неотрицательными членами.
Определение. Знакочередующийся ряд вида
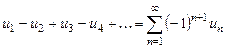 ,
,
где числа 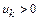 , монотонно убывая, стремятся к нулю
, монотонно убывая, стремятся к нулю 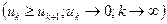 , называется рядом Лейбница.
, называется рядом Лейбница.
Теорема 11.2. Ряд Лейбница сходится и его сумма 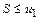
Если ряд сходится абсолютно, то при любой перестановке его членов сходимость ряда не нарушается и его сумма остаётся прежней.
Пример 11.7. Исследовать на абсолютную и условную сходимость ряд 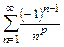 .
.
Решение. Сначала изучим ряд 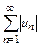 . В нашем случае
. В нашем случае 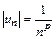 . Если
. Если 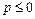 , то
, то 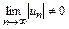 и, значит, ряд
и, значит, ряд 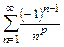 расходится. При
расходится. При 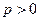 возможны два варианта: а) если
возможны два варианта: а) если 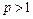 то ряд
то ряд 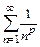 сходится (см. пример 11.1), откуда следует, что ряд
сходится (см. пример 11.1), откуда следует, что ряд 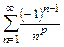 сходится абсолютно; б) если
сходится абсолютно; б) если 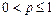 , то ряд
, то ряд 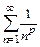 расходится, значит, исходный ряд не будет сходиться абсолютно. Исследуем его на условную сходимость. Докажем, что ряд является рядом Лейбница. Действительно,
расходится, значит, исходный ряд не будет сходиться абсолютно. Исследуем его на условную сходимость. Докажем, что ряд является рядом Лейбница. Действительно, 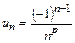
 , т.е. ряд знакочередующийся, последовательность
, т.е. ряд знакочередующийся, последовательность 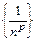 убывающая,
убывающая, 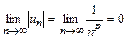 . Согласно признаку Лейбница ряд сходится.
. Согласно признаку Лейбница ряд сходится.
Таким образом, мы доказали, что исследуемый ряд 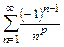 расходится, если
расходится, если  , сходится абсолютно, если
, сходится абсолютно, если 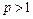 , и сходится условно, если
, и сходится условно, если 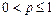 .
.
Контрольные вопросы.
- Сформулируйте признак Даламбера.
- Сформулируйте признак Коши.
- Сформулируйте интегральный признак Коши.
- Дайте определение абсолютно сходящегося ряда. Сходится ли ряд, сходящийся абсолютно? В каком случае ряд называется условно сходящимся?
- Дайте определение ряда Лейбница. Сформулируйте теорему о сходимости и сумме ряда Лейбница.

 с неотрицательными членами существует предел
с неотрицательными членами существует предел 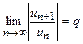 , то этот ряд сходится при
, то этот ряд сходится при 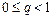 и расходится при
и расходится при 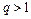 . Случай
. Случай 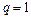 требует дополнительного исследования. При
требует дополнительного исследования. При 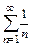 расходится, а ряд
расходится, а ряд  сходится, хотя для обоих этих рядов
сходится, хотя для обоих этих рядов 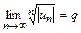 , то этот ряд сходится при
, то этот ряд сходится при 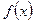 при
при 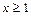 непрерывная, неотрицательная и монотонно убывающая функция, то ряд с неотрицательными членами
непрерывная, неотрицательная и монотонно убывающая функция, то ряд с неотрицательными членами  , где
, где 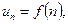 сходится или расходится вместе с несобственным интегралом
сходится или расходится вместе с несобственным интегралом 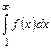 .
.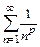 (11.1)
(11.1)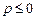 не выполняется необходимый признак сходимости (теорема 9.2), следовательно, ряд расходится. Члены ряда (11.1) являются значениями функции
не выполняется необходимый признак сходимости (теорема 9.2), следовательно, ряд расходится. Члены ряда (11.1) являются значениями функции 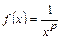 в точках
в точках 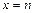 . Функция
. Функция 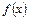 неотрицательна и монотонно убывает (если
неотрицательна и монотонно убывает (если  ) при
) при 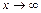 , поэтому ряд (11.1) сходится или расходится вместе с несобственным интегралом
, поэтому ряд (11.1) сходится или расходится вместе с несобственным интегралом 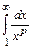 . При
. При  имеем
имеем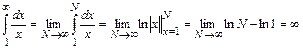 ,
,
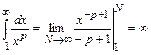 ,
,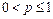 ряд Дирихле расходится. Если же
ряд Дирихле расходится. Если же 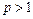 , то
, то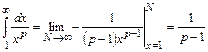 ,
,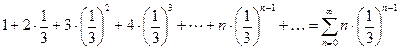 .
. ,
,  .
.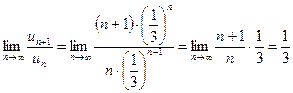 ,
,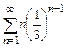 сходится.
сходится.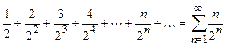 .
.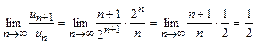 .
.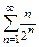 сходится.
сходится.
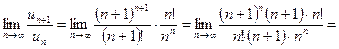
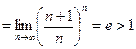 .
.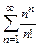 расходится.
расходится.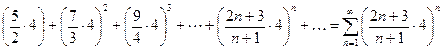 .
.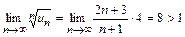 ,
,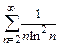 .
.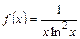 неотрицательна и убывает при
неотрицательна и убывает при 
 , т.е.
, т.е. 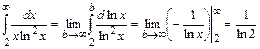
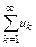 (11.1)
(11.1)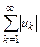 . (11.2)
. (11.2)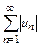 .
.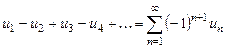 ,
,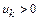 , монотонно убывая, стремятся к нулю
, монотонно убывая, стремятся к нулю 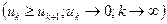 , называется рядом Лейбница.
, называется рядом Лейбница.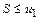
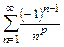 .
.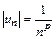 . Если
. Если 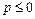 , то
, то 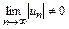 и, значит, ряд
и, значит, ряд 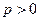 возможны два варианта: а) если
возможны два варианта: а) если 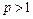 то ряд
то ряд 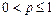 , то ряд
, то ряд 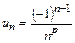
 , т.е. ряд знакочередующийся, последовательность
, т.е. ряд знакочередующийся, последовательность 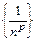 убывающая,
убывающая, 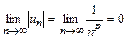 . Согласно признаку Лейбница ряд сходится.
. Согласно признаку Лейбница ряд сходится. , сходится абсолютно, если
, сходится абсолютно, если 


