На дом № 2842,2844, 2846, 2856, 2860, 2864.
Важным случаем функциональных рядов являются степенные ряды:
или
Для выяснения свойств степенных рядов достаточно ограничиться рассмотрением рядов вида (12.1), так как ряд по степеням Теорема 12.1. (Абеля)Пусть степенной ряд (12.1) сходится в точке Для определения области сходимости степенного ряда используется либо признак Даламбера, либо признак Коши. Рассмотрим степенной ряд
Вычислим предел
Если существует предел (12.3), то ряд (12.2) сходится, если
и расходится, если
Определение. Число Формула для радиуса сходимости, получаемая с помощью признака Даламбера, имеет вид
Если же к ряду (12.2) применить признак Коши, то получим соотношение
из которого следует, что ряд (12.2) сходится, если
которая носит название формулы Коши – Адамара. Пример 12.1. Найти область сходимости ряда
Решение. По признаку Даламбера:
что означает, что ряд сходится на всей оси Х.
Пример 12.2. Найти область сходимости ряда
Решение. По формуле Коши – Адамара (12.5) находим
т.е. ряд сходится в области
т.е. необходимый признак сходимости не выполнен, следовательно, в точке
Пример 12.3. Найти область сходимости ряда
Решение. Следует отметить, что формула (12.4) для радиуса сходимости выведена в предположении, что степенной ряд (12.1) содержит все степени переменной х. В нашем случае равны нулю коэффициенты при чётных степенях, поэтому
т.е. формулу (12.4) применить нельзя. Однако применение признака Даламбера возможно и приводит к соотношению
Это означает, что ряд (12.6) сходится, если
Согласно второму признаку сравнения этот ряд расходится вместе с гармоническим рядом, с которым производится сравнение:
При
Пример 12.4. Найти область сходимости ряда
Решение. Степени
Степенной ряд сходится равномерно при Теорема 12.2. В области равномерной сходимости Теорема 12.3. В области равномерной сходимости
сходится в той же области Пример 12.5. Найти сумму ряда
Решение. Обозначим сумму ряда через
После интегрирования получим
Контрольные вопросы.
|

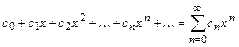 (12.1)
(12.1) .
.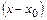 легко свести к виду (12.1) заменой переменной
легко свести к виду (12.1) заменой переменной  , т.е. переносом начала координат в точку
, т.е. переносом начала координат в точку 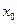 . Для нахождения области сходимости степенного ряда сформулируем следующую теорему.
. Для нахождения области сходимости степенного ряда сформулируем следующую теорему.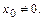 Тогда он сходится абсолютно в любой точке х, для которой
Тогда он сходится абсолютно в любой точке х, для которой  и равномерно в любой области
и равномерно в любой области  . Если степенной ряд (12.1) расходится в точке
. Если степенной ряд (12.1) расходится в точке  , то он расходится и во всех точках
, то он расходится и во всех точках 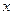 таких, что
таких, что  .
. . (12.2)
. (12.2)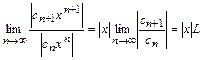 . (12.3)
. (12.3) , и расходится, если
, и расходится, если  . Следовательно, ряд (12.1) сходится абсолютно, если
. Следовательно, ряд (12.1) сходится абсолютно, если ,
, .
. такое, что для всех x, удовлетворяющих условию
такое, что для всех x, удовлетворяющих условию 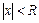 , ряд (12.2) сходится, а для всех х, удовлетворяющих условию
, ряд (12.2) сходится, а для всех х, удовлетворяющих условию 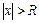 , ряд расходится, называется радиусом сходимости ряда (12.1).
, ряд расходится, называется радиусом сходимости ряда (12.1). (12.4)
(12.4) ,
, , расходится, если
, расходится, если 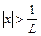 , а радиус сходимости ряда (12.1) определяется по формуле
, а радиус сходимости ряда (12.1) определяется по формуле , (12.5)
, (12.5)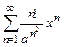 при
при  .
.

 ,
,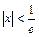 . При
. При  получаем
получаем ,
, исследуемый ряд расходится. Расходимость ряда в точке
исследуемый ряд расходится. Расходимость ряда в точке 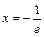 доказывается аналогично.
доказывается аналогично. . (12.6)
. (12.6)
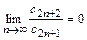 ,
,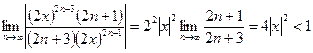 .
. , т.е. в области
, т.е. в области  В точке
В точке 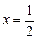 общий член ряда
общий член ряда .
. :
: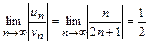 .
.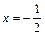 исследуемый ряд принимает вид
исследуемый ряд принимает вид 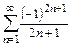 и сходится как ряд Лейбница. Следовательно, промежуток сходимости ряда:
и сходится как ряд Лейбница. Следовательно, промежуток сходимости ряда:  . Причем при
. Причем при  ряд сходится условно, а при
ряд сходится условно, а при  абсолютно.
абсолютно.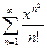 . (12.7)
. (12.7)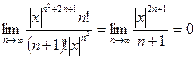 при
при  .
. , причем число
, причем число  как угодно близко к радиусу сходимости
как угодно близко к радиусу сходимости 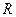 , но не равно ему. Поэтому для степенных рядов справедливы следующие утверждения.
, но не равно ему. Поэтому для степенных рядов справедливы следующие утверждения. r степенной ряд (12.1) можно почленно дифференцировать любое число раз, причем радиусы сходимости получаемых рядов также равны r.
r степенной ряд (12.1) можно почленно дифференцировать любое число раз, причем радиусы сходимости получаемых рядов также равны r.
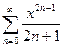 ,
, 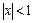 .
. и продифференцируем ряд почленно:
и продифференцируем ряд почленно: при
при  при
при 


