Пусть 
есть векторное пространство над полем 
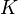и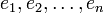 
— базис в .
Функция 
называется квадратичной формой, если её можно представить в виде
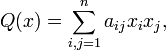
где 
, а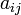 
— некоторые элементы поля .
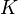Квадратичные формы.
Определение. Квадратичной формой или квадратичной функцией на линейном пространстве L называется функция к, значение которой на любом векторе х определяется равенством k(х) = b(x,x), где b — симметричная билинейная функция.
По заданной квадратичной форме к однозначно определяется соответствующая симметричная билинейная функция b. Действительно, пусть х и у — произвольные векторы. Тогда
k(х + у) = b(х + у, х + у) = b(х, х) + b(х, у) + b(у, х) + b(у, у).
Отсюда, используя b(y,x) = b(x,y), получаем, что значение b на любых векторах выражается через значения k.
Матрицей квадратичной формы называется матрица соответствующей билинейной функции.
Из ранее выведенного мы имеем следующее выражение значения квадратичной формы через координатный столбец вектора: k(x) = 
.
Замена базиса в данном случае очевидным образом следует из замены базиса в билинейной форме.
