Вопрос39 Критерий Сильвестра положительной определенности квадратичной формы.
Критерий Сильвестра · Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны. · Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен. · Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой. · Пусть квадратичная форма имеет в каком-то базисе матрицу · · Тогда эта форма положительно определена, тогда и только тогда когда все её главные (угловые) миноры · · · · Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица · · не является неотрицательно определённой — так как, например,
|
положительны. Форма отрицательно определена, если и только если знаки 
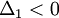. Здесь главными минорами матрицы 
называются определители вида
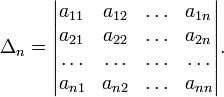
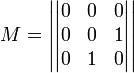
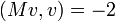для 
. В то же время все её главные миноры равны 0, то есть неотрицательны.
