Преобразование матрицы линейного оператора при изменении базиса
Как уже отмечалось, в пространстве Rn существует множество различных базисов. Пусть Обозначим
Тогда
откуда имеем
Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f, A = { a i j } = { A (e j) i }:
Координаты образа y = A (x) и прообраза x связаны соотношеннием: y = A · x,
Вопрос 32 Приведение матрицы линейного оператора к диагональной форме Таким образом можно описать алгоритм приведения матрицы линейного оператора к диагональной форме. Он состоит в следующем: · записываем матрицу оператора A в исходном базисе; · записываем характеристическое уравнение и вычисляем его корни; · находим собственный базис оператора (если он существует); · записываем матрицу C, столбцами которой являются координаты собственных векторов (векторов собственного базиса); · по формуле C-1AC находим диагональную форму матриц оператора — матрицу оператора в собственном базисе.
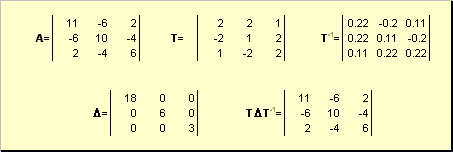
Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия — A = TΛT −1 Здесь Λ; = diag(λ1,..., λ N) — это диагональная матрица, элементами которой являются собственные значения матрицы A, а T — это матрица, составленная из соответствующих собственных векторов матрицы A, т.е. T = (v 1,..., v N). Например,
|

 и
и 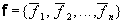 — двабазиса в Rn.
— двабазиса в Rn.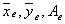 и
и  координаты векторов
координаты векторов 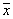 и
и 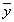 из Rn и матрицу оператора A соответственно в базисах
из Rn и матрицу оператора A соответственно в базисах 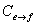 — матрица перехода от базиса
— матрица перехода от базиса  ,
, ,
,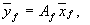
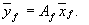

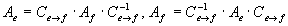 — формулы преобразования матрицы линейного оператора при изменении базиса.
— формулы преобразования матрицы линейного оператора при изменении базиса.