Общее решение систем линейных уравнений. Главные и свободные неизвестные.
Определение 5.1. Системой m линейных уравнений с n неизвестными где Определение 5.2. Решением системы Определение 5.3. Система Определение 5.4. Совместная система Определение 5.5. Матрица Матрица называется расширенной матрицей этой системы. Замечание. Система где Определение 5.6. Если все свободные члены системы уравнений равны нулю, то такая система называется однородной, если же хотя бы один свободный член отличен от нуля, система называется неоднородной. Теорема 5.1. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда определитель основной матрицы системы равен нулю. Определение 5.7. Элементарными преобразованиями системы линейных уравнений называют следующие операции: 1) сложение обеих частей одного уравнения с соответствующими частями другого, умноженных на одно и то же число, не равное нулю; 2) перестановка уравнений местами; 3) удаление из системы уравнений, являющихся тождествами. Рассмотрим основные методы решения систем линейных уравнений.
|

 называется система S вида
называется система S вида ,
,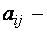 коэффициенты при неизвестных,
коэффициенты при неизвестных,  свободные члены (
свободные члены (  ,
,  заданные числа).
заданные числа). называется упорядоченный набор действительных чисел
называется упорядоченный набор действительных чисел  , при подстановке которых в каждое уравнение системы вместо
, при подстановке которых в каждое уравнение системы вместо  соответственно будут получены верные числовые равенства.
соответственно будут получены верные числовые равенства. называется совместной (несовместной), если она имеет хотя бы одно решение (не имеет решений).
называется совместной (несовместной), если она имеет хотя бы одно решение (не имеет решений). , составленная из коэффициентов при неизвестных, называется основной матрицей системы
, составленная из коэффициентов при неизвестных, называется основной матрицей системы 

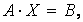
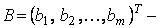 вектор-столбец свободных членов системы.
вектор-столбец свободных членов системы.


