В предыдущем разделе были введены операции умножения матриц на число и сложения матриц, в частности, для матриц-столбцов 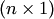 и матриц-строк
и матриц-строк  . Матрицы-столбцы (матрицы-строки) будем называть далее просто столбцами (соответственно строками) и обозначать в этой главе прописными буквами. При помощи этих операций можно составлять некоторые алгебраические выражения. Напомним, что равными считаются столбцы одинаковых размеров с равными соответствующими элементами.
. Матрицы-столбцы (матрицы-строки) будем называть далее просто столбцами (соответственно строками) и обозначать в этой главе прописными буквами. При помощи этих операций можно составлять некоторые алгебраические выражения. Напомним, что равными считаются столбцы одинаковых размеров с равными соответствующими элементами.
Столбец  называется линейной комбинацией столбцов
называется линейной комбинацией столбцов  одинаковых размеров, если
одинаковых размеров, если

где  — некоторые числа. В этом случае говорят, что столбец
— некоторые числа. В этом случае говорят, что столбец  разложен по столбцам
разложен по столбцам  , а числа
, а числа  называют коэффициентами разложения. Линейная комбинация
называют коэффициентами разложения. Линейная комбинация  с нулевыми коэффициентами называется тривиальной.
с нулевыми коэффициентами называется тривиальной.
Если столбцы в (3.1) имеют вид
то матричному равенству (3.1) соответствуют поэлементные равенства
Аналогично формулируется определение линейной комбинации строк одинаковых размеров.
Набор столбцов  одинаковых размеров называется системой столбцов.
одинаковых размеров называется системой столбцов.
Система из  столбцов
столбцов  называется линейно зависимой, если существуют такие числа
называется линейно зависимой, если существуют такие числа  , не все равные нулю одновременно, что
, не все равные нулю одновременно, что

Здесь и далее символом о обозначается нулевой столбец соответствующих размеров.
Система из  столбцов
столбцов  называется линейно независимой, если равенство (3.2) возможно только при
называется линейно независимой, если равенство (3.2) возможно только при 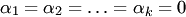 , т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).
, т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).

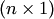 и матриц-строк
и матриц-строк  . Матрицы-столбцы (матрицы-строки) будем называть далее просто столбцами (соответственно строками) и обозначать в этой главе прописными буквами. При помощи этих операций можно составлять некоторые алгебраические выражения. Напомним, что равными считаются столбцы одинаковых размеров с равными соответствующими элементами.
. Матрицы-столбцы (матрицы-строки) будем называть далее просто столбцами (соответственно строками) и обозначать в этой главе прописными буквами. При помощи этих операций можно составлять некоторые алгебраические выражения. Напомним, что равными считаются столбцы одинаковых размеров с равными соответствующими элементами. называется линейной комбинацией столбцов
называется линейной комбинацией столбцов  одинаковых размеров, если
одинаковых размеров, если
 — некоторые числа. В этом случае говорят, что столбец
— некоторые числа. В этом случае говорят, что столбец  с нулевыми коэффициентами называется тривиальной.
с нулевыми коэффициентами называется тривиальной. столбцов
столбцов 
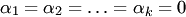 , т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).
, т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).


