Решение. Так как правила сложения и умножения для многочленов те же самые, что и для целых чисел (аксиомы кольца)
Так как правила сложения и умножения для многочленов те Начальная установка: m(х) = х4 - зх2 - 4, n(х) = хЗ + х2 + 4,
Деление: х4 - зх2 - 4 = (х - 1). (хЗ + х2 + 4) - 2х2 - 4х, q(x) = х - 1. Пересчет 6 величин: m(х) = хЗ + х2 + 4, n(х) = -2х2 - 4х, Заметим, что по определению наибольшего общего делителя
На основании этого изменим вычислительную схему следующим С учетом этого замечания, продолжим вычисления со следующими 6 многочленами:
(Многочлены n(х),
Пересчет 6 величин:
Деление на старший коэффициент:
При следующем делении х2 +2х = х(х+2) получаем нулевой
Задачи для самостоятельного решения Найти наибольший общий делитель
если
1)
|
(х) = 
, v(x) = 
, 
= 
= 1.
= 
)=1, 
, 
, 
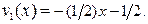
+ х2 + 4 = (х - 1). (х2 + 2х) + 2х + 4, q(x) = х - 1.
, 
, 
многочленов 
и 
из кольца 
и его представление в форме
, 
,
, 
, 2) 
, 
.
