Решение. Для решения задачи воспользуемся теорией Фредгольма
Для решения задачи воспользуемся теорией Фредгольма. Для этого запишем 4 системы: 1) 2) 3) 4) Здесь Теорема1. Следующие четыре условия эквивалентны: а) система 1) имеет решение (единственное) при любой правой части у; б) система 2) имеет только нулевое решение; в) система 3) имеет решение (единственное) при любой правой части у; г) система 4) имеет только нулевое решение. Эквивалентность первого и четвертого утверждений известна, как альтернатива Фредгольма: либо система 1) имеет единственное решение для любой правой части, либо система 4) имеет не нулевое решение. Теорема 2. Системы 2), 4) имеют одинаковое число линейно независимых решений. Теорема 3. Система 1) имеет хотя бы одно решение тогда и только тогда, когда правая часть у ортогональна всем решениям уравнения 4). Исследуем систему 4). Так как
Эта система имеет ненулевое решение только в случае, когда
Вычисляя определитель, получим квадратное уравнение
Таким образом, при Если Пусть теперь
|

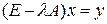 ,
,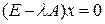 ,
,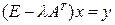 ,
,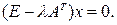
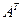 - транспонированная матрица. Теория Фредгольма сводится к трем утверждениям:
- транспонированная матрица. Теория Фредгольма сводится к трем утверждениям: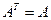 , то оно запишется в следующем виде
, то оно запишется в следующем виде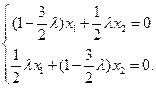
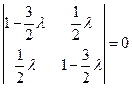 .
.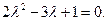 Его корни
Его корни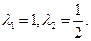
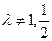 система 1) имеет единственное решение для любой правой части у.
система 1) имеет единственное решение для любой правой части у.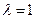 , то система 4) сводится к одному уравнению
, то система 4) сводится к одному уравнению 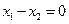 . Оно имеет одно линейно независимое решение
. Оно имеет одно линейно независимое решение 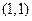 . По теоремам 1, 3 при
. По теоремам 1, 3 при 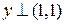 система 1) имеет бесконечно много решений, а при
система 1) имеет бесконечно много решений, а при 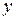 , не ортогональном вектору
, не ортогональном вектору 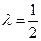 . В этом случае система 4) сводится к уравнению
. В этом случае система 4) сводится к уравнению  Оно имеет одно линейно независимое решение
Оно имеет одно линейно независимое решение 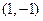 . По теоремам 1, 3 при
. По теоремам 1, 3 при 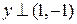 система 1) имеет бесконечно много решений, а при
система 1) имеет бесконечно много решений, а при 


