Изоморфизмомполей  и
и  называется отображение
называется отображение

одного поля на другое, при которой сохраняются операции:
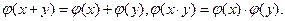
Из этого определения можно вывести такие простые следствия. Так как нулевой элемент поля определяется аксиомой
х + 0 = х,
то, применив к этому равенству отображение  , получим
, получим
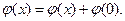
Так как  — биекция. то когда х пробегает одно поле,
— биекция. то когда х пробегает одно поле,  пробегает другое. Следовательно,
пробегает другое. Следовательно,  - нулевой элемент второго поля, то есть при изоморфизме ноль должен отображаться в ноль. Совершенно так же устанавливается, что единица отображается в единицу. (Если характеристика поля р > 2, то, продолжая рассуждение, можно установить, что каждый элемент простого подполя
- нулевой элемент второго поля, то есть при изоморфизме ноль должен отображаться в ноль. Совершенно так же устанавливается, что единица отображается в единицу. (Если характеристика поля р > 2, то, продолжая рассуждение, можно установить, что каждый элемент простого подполя  отображается в себя).
отображается в себя).
Элементами поля  являются многочлены 4-й степени от
являются многочлены 4-й степени от  с коэффициентами из
с коэффициентами из  :
:
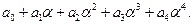
Элементы поля  — такие же многочлены от
— такие же многочлены от 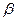 . Пусть
. Пусть  — искомый изоморфизм, тогда из определения изоморфизма и указанных простых следствий получим
— искомый изоморфизм, тогда из определения изоморфизма и указанных простых следствий получим
 (1)
(1)
Таким образом, изоморфизм  полностью определяется заданием образа элемента
полностью определяется заданием образа элемента  .
.
Выясним каким должен быть этот образ. Так как
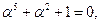
то в силу изоморфизма должно выполняться

Многочлен  , корнем которого является
, корнем которого является  и
и  , это минимальный многочлен этих элементов. Итак, при изоморфизме образующий элемент
, это минимальный многочлен этих элементов. Итак, при изоморфизме образующий элемент  первого поля должен отображаться в элемент второго поля, имеющий тот же самый минимальный многочлен.
первого поля должен отображаться в элемент второго поля, имеющий тот же самый минимальный многочлен.
Обратно, пусть  и
и  . Так как многочлен
. Так как многочлен  неприводим, то элементы поля
неприводим, то элементы поля 
 линейно независимы (над
линейно независимы (над  ) и все элементы
) и все элементы  могут быть представлены как многочлены 4-й степени от
могут быть представлены как многочлены 4-й степени от  . Эти многочлены складываются и перемножаются по обычным правилам с заменой
. Эти многочлены складываются и перемножаются по обычным правилам с заменой  на
на  . То есть
. То есть  и
и  отличаются только обозначением образующего элемента и их изоморфизм очевиден.
отличаются только обозначением образующего элемента и их изоморфизм очевиден.
Замечание. Набор минимальных многочленов элементов конечного поля из рп элементов определяется однозначно, независимо от того, как построено поле. — это неприводимые делители многочлена деления круга  . Поэтому для каждого элемента одного поля всегда найдется элемент другого, имеющий тот же самый минимальный многочлен. Отсюда, в частности, вытекает, что два конечных поля с одинаковым числом элементов всегда изоморфны.
. Поэтому для каждого элемента одного поля всегда найдется элемент другого, имеющий тот же самый минимальный многочлен. Отсюда, в частности, вытекает, что два конечных поля с одинаковым числом элементов всегда изоморфны.
Итак, чтобы установить требуемый изоморфизм, надо в поле  найти корень многочлена
найти корень многочлена  .
.
Один из способов решения этой задачи - подставить элемент  с неопределенными коэффициентами в многочлен:
с неопределенными коэффициентами в многочлен:
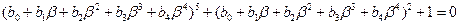
После выполнения в левой части действий по законам поля  (то есть с заменой
(то есть с заменой  на
на  ) получается система относительно коэффициентов, которую можно решить, перебирая 32 возможных набора этих коэффициентов.
) получается система относительно коэффициентов, которую можно решить, перебирая 32 возможных набора этих коэффициентов.
В виду некоторой сложности этого способа в данном примере (для других полей он может оказаться вполне приемлемым), будем решать поставленную задачу иначе: просматривать по очереди элементы  и определять их минимальные многочлены, пока не встретим нужного.
и определять их минимальные многочлены, пока не встретим нужного.
Для вычислений удобно предварительно составить таблицу поля  (см. таблицу).
(см. таблицу).
Поле  ,
, 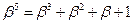
Элемент 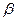 является корнем многочлена
является корнем многочлена
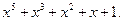
Остальными корнями этого многочлена являются элементы
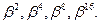
Эти элементы далее не рассматриваем.
Найдем минимальный многочлен элемента  . Используя таблицу поля, вычислим последовательные степени
. Используя таблицу поля, вычислим последовательные степени  :
:

Умножая эти равенства на указанные слева коэффициенты и приравнивая нулю коэффициенты при  , …,
, …,  в правой части, получаем линейную систему для
в правой части, получаем линейную систему для  :
:
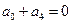
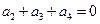
а2=0

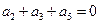
Учитывая, что а0 = 1 (иначе получится приводимый многочлен) без труда находим решение
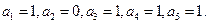
Таким образом, минимальным многочленом элемента  является многочлен
является многочлен  . Остальные его корни —
. Остальные его корни — 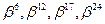 — в дальнейших пробах не участвуют.
— в дальнейших пробах не участвуют.
Найдем минимальный многочлен элемента  Действуя
Действуя
аналогично имеем
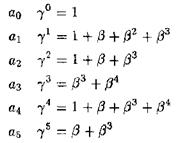
Система
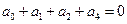
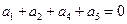
 =0
=0
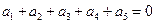

Снова полагая а0 = 1, находим решение
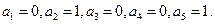
Таким образом, минимальным многочленом элемента  является многочлен
является многочлен  Он совпадает с минимальным многочленом элемента а из поля рь Следовательно, нужный изоморфизм
Он совпадает с минимальным многочленом элемента а из поля рь Следовательно, нужный изоморфизм  получится, если положить
получится, если положить  Образ любого элемента можно вычислить с помощью соотношения (1).
Образ любого элемента можно вычислить с помощью соотношения (1).

 и
и  называется отображение
называется отображение
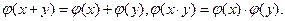
 , получим
, получим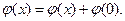
 пробегает другое. Следовательно,
пробегает другое. Следовательно,  - нулевой элемент второго поля, то есть при изоморфизме ноль должен отображаться в ноль. Совершенно так же устанавливается, что единица отображается в единицу. (Если характеристика поля р > 2, то, продолжая рассуждение, можно установить, что каждый элемент простого подполя
- нулевой элемент второго поля, то есть при изоморфизме ноль должен отображаться в ноль. Совершенно так же устанавливается, что единица отображается в единицу. (Если характеристика поля р > 2, то, продолжая рассуждение, можно установить, что каждый элемент простого подполя  отображается в себя).
отображается в себя). с коэффициентами из
с коэффициентами из  :
: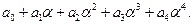
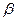 . Пусть
. Пусть  (1)
(1)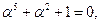

 , корнем которого является
, корнем которого является  , это минимальный многочлен этих элементов. Итак, при изоморфизме образующий элемент
, это минимальный многочлен этих элементов. Итак, при изоморфизме образующий элемент  и
и  . Так как многочлен
. Так как многочлен  линейно независимы (над
линейно независимы (над  ) и все элементы
) и все элементы  . Эти многочлены складываются и перемножаются по обычным правилам с заменой
. Эти многочлены складываются и перемножаются по обычным правилам с заменой  на
на  . То есть
. То есть  . Поэтому для каждого элемента одного поля всегда найдется элемент другого, имеющий тот же самый минимальный многочлен. Отсюда, в частности, вытекает, что два конечных поля с одинаковым числом элементов всегда изоморфны.
. Поэтому для каждого элемента одного поля всегда найдется элемент другого, имеющий тот же самый минимальный многочлен. Отсюда, в частности, вытекает, что два конечных поля с одинаковым числом элементов всегда изоморфны.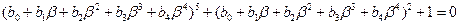
 на
на  ) получается система относительно коэффициентов, которую можно решить, перебирая 32 возможных набора этих коэффициентов.
) получается система относительно коэффициентов, которую можно решить, перебирая 32 возможных набора этих коэффициентов.
 ,
, 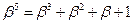
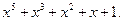
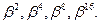
 . Используя таблицу поля, вычислим последовательные степени
. Используя таблицу поля, вычислим последовательные степени 
 , …,
, …,  в правой части, получаем линейную систему для
в правой части, получаем линейную систему для  :
: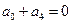
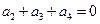

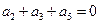
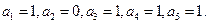
 является многочлен
является многочлен  . Остальные его корни —
. Остальные его корни — 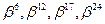 — в дальнейших пробах не участвуют.
— в дальнейших пробах не участвуют. Действуя
Действуя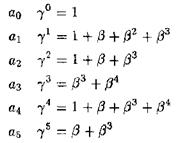
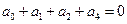
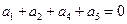
 =0
=0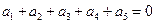

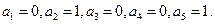
 Он совпадает с минимальным многочленом элемента а из поля рь Следовательно, нужный изоморфизм
Он совпадает с минимальным многочленом элемента а из поля рь Следовательно, нужный изоморфизм  Образ любого элемента можно вычислить с помощью соотношения (1).
Образ любого элемента можно вычислить с помощью соотношения (1).


