Для матрицы  найти сингулярные числа и получить сингулярное и полярное разложения.
найти сингулярные числа и получить сингулярное и полярное разложения.
Решение
Сингулярные числа матрицы  - это квадратные корни из собственных значений матрицы
- это квадратные корни из собственных значений матрицы
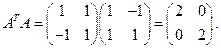
Таким образом, сингулярные числа равны 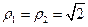 . Сингулярное разложение матрицы имеет вид
. Сингулярное разложение матрицы имеет вид 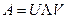 , где
, где  - ортогональные матрицы,
- ортогональные матрицы,
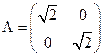
- диагональная матрица с сингулярными числами на главной диагонали. Матрицы 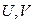 строятся с помощью сингулярных базисов. Матрица
строятся с помощью сингулярных базисов. Матрица  - симметричная и у нее существует ортонормированный базис из собственных векторов. В нашем случае это
- симметричная и у нее существует ортонормированный базис из собственных векторов. В нашем случае это  Он образует первый сингулярный базис. Второй сингулярный ортонормированный базис образуют векторы
Он образует первый сингулярный базис. Второй сингулярный ортонормированный базис образуют векторы

Столбцы матрицы  образуют координаты второго сингулярного базиса, а столбцы матрицы
образуют координаты второго сингулярного базиса, а столбцы матрицы  - первого сингулярного базиса. Имеем
- первого сингулярного базиса. Имеем
 ,
,
Поэтому сингулярное разложение матрицы  имеет вид
имеет вид
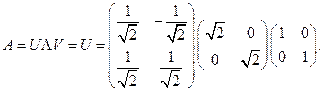
Полярное разложение матрицы  - это ее представление в виде произведения
- это ее представление в виде произведения 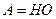 , где
, где  - эрмитова (симметричная) матрица, а
- эрмитова (симметричная) матрица, а  - ортогональная матрица. Его можно получить из сингулярного разложения:
- ортогональная матрица. Его можно получить из сингулярного разложения:  Итак, полярное разложение имеет вид
Итак, полярное разложение имеет вид

Задачи для самостоятельного решения
1. Для матрицы  найти сингулярные числа и получить сингулярное и полярное разложения.
найти сингулярные числа и получить сингулярное и полярное разложения.
2. Для матрицы 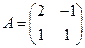 найти сингулярные числа и получить сингулярное и полярное разложения.
найти сингулярные числа и получить сингулярное и полярное разложения.

 найти сингулярные числа и получить сингулярное и полярное разложения.
найти сингулярные числа и получить сингулярное и полярное разложения. - это квадратные корни из собственных значений матрицы
- это квадратные корни из собственных значений матрицы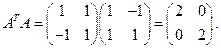
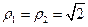 . Сингулярное разложение матрицы имеет вид
. Сингулярное разложение матрицы имеет вид 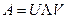 , где
, где  - ортогональные матрицы,
- ортогональные матрицы,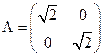
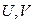 строятся с помощью сингулярных базисов. Матрица
строятся с помощью сингулярных базисов. Матрица  - симметричная и у нее существует ортонормированный базис из собственных векторов. В нашем случае это
- симметричная и у нее существует ортонормированный базис из собственных векторов. В нашем случае это  Он образует первый сингулярный базис. Второй сингулярный ортонормированный базис образуют векторы
Он образует первый сингулярный базис. Второй сингулярный ортонормированный базис образуют векторы
 образуют координаты второго сингулярного базиса, а столбцы матрицы
образуют координаты второго сингулярного базиса, а столбцы матрицы  - первого сингулярного базиса. Имеем
- первого сингулярного базиса. Имеем ,
,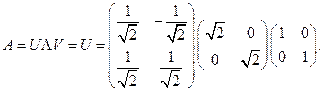
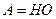 , где
, где  - эрмитова (симметричная) матрица, а
- эрмитова (симметричная) матрица, а  - ортогональная матрица. Его можно получить из сингулярного разложения:
- ортогональная матрица. Его можно получить из сингулярного разложения:  Итак, полярное разложение имеет вид
Итак, полярное разложение имеет вид
 найти сингулярные числа и получить сингулярное и полярное разложения.
найти сингулярные числа и получить сингулярное и полярное разложения.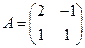 найти сингулярные числа и получить сингулярное и полярное разложения.
найти сингулярные числа и получить сингулярное и полярное разложения.


