Элементы поля 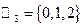 будем обозначать
будем обозначать  , так как
, так как 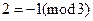 . Многочлен 3-й степени имеет вид
. Многочлен 3-й степени имеет вид
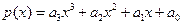 ,
,
где  и
и 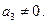 Так как многочлены, полу-
Так как многочлены, полу-
чающиеся один из другого умножением на не нулевую константу
(то есть на -1), естественно не различать, то будем считать, что
 . Если
. Если  , то многочлен разложим
, то многочлен разложим
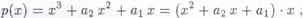
поэтому  .
.
Итак, будем далее рассматривать многочлены вида
 (2)
(2)
Нетрудно подсчитать, что таких многочленов 18 штук. Чтобы
выбрать среди них неприводимые, заметим, что если многочлен
3-й степени приводим, то он представляется в виде произведения
многочленов 1-й и 2-й степени:
 .
.
в этом случае число 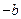 будет корнем многочлена. Обратно,
будет корнем многочлена. Обратно,
если многочлен 3-й степени имеет корень 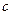 в поле
в поле  , то он
, то он
по теореме Безу делится на 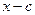 и, следовательно, приводим.
и, следовательно, приводим.
Таким образом, из 18 многочленов вида (2) надо отбросить те, ко-
торые имеют корень в поле  . Так как
. Так как 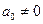 , то
, то  не является
не является
корнем этих многочленов и будем далее проверять только ±1.
Разделим  многочленов на два класса: с
многочленов на два класса: с  и с
и с  .
.
1.  . (3)
. (3)
Для многочленов вида (3), имеющих корень  , имеем
, имеем
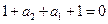 или
или 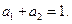
Этому условию удовлетворяют следующие пары  :
:
 (4)
(4)
Для многочленов вида (3), имеющих корень  , имеем
, имеем
 или
или 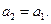
Этому условию удовлетворяют следующие пары  :
:
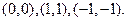 (5)
(5)
2.  (6)
(6)
Для многочленов вида (6), имеющих корень  , имеем
, имеем
 или
или 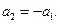
Этому условию удовлетворяют следующие пары  :
:
 (7)
(7)
Для многочленов вида (6), имеющих корень  , имеем
, имеем
 или
или 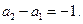
Этому условию удовлетворяют следующие пары  :
:
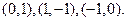 (8)
(8)
Отбрасывая многочлены, коэффициенты которых встречаются в списках (4), (5) и (7), (8), получаем следующие 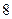 неприводимых многочленов
неприводимых многочленов
 ,
,


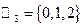 будем обозначать
будем обозначать  , так как
, так как 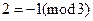 . Многочлен 3-й степени имеет вид
. Многочлен 3-й степени имеет вид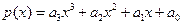 ,
, и
и 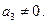 Так как многочлены, полу-
Так как многочлены, полу-  . Если
. Если  , то многочлен разложим
, то многочлен разложим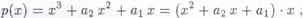
 .
. (2)
(2) .
.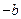 будет корнем многочлена. Обратно,
будет корнем многочлена. Обратно, 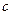 в поле
в поле  , то он
, то он 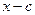 и, следовательно, приводим.
и, следовательно, приводим.  . Так как
. Так как 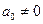 , то
, то  не является
не является  многочленов на два класса: с
многочленов на два класса: с  и с
и с  .
. . (3)
. (3) , имеем
, имеем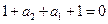 или
или 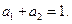
 :
: (4)
(4) , имеем
, имеем или
или 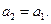
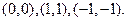 (5)
(5) (6)
(6) или
или 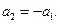
 (7)
(7) или
или 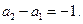
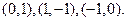 (8)
(8) неприводимых многочленов
неприводимых многочленов ,
,



