Кодом длины п называется произвольное подмножество 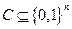 . Различаются коды по двум их основным характеристикам:
. Различаются коды по двум их основным характеристикам:
-  , этот параметр определяет скорость передачи информации по каналу связи: если канал передает 1 бит за единицу времени, то кодированную информацию канал будет передавать с меньшей скоростью
, этот параметр определяет скорость передачи информации по каналу связи: если канал передает 1 бит за единицу времени, то кодированную информацию канал будет передавать с меньшей скоростью 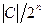 бит за единицу времени.
бит за единицу времени.
- 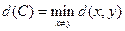 — кодовое расстояние, этот параметр определяет возможности исправления ошибок кодом С: если
— кодовое расстояние, этот параметр определяет возможности исправления ошибок кодом С: если  (С) > 2е, то код исправляет е ошибок.
(С) > 2е, то код исправляет е ошибок.
Для построения кодов на множестве двоичных слов 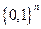 вводят различные алгебраические структуры: с их помощью дается описание кода и исследуются его параметры.
вводят различные алгебраические структуры: с их помощью дается описание кода и исследуются его параметры.
Такой структурой для кодов Боуза, Чаудхури, Хоквингема (БЧХ-кодов) является кольцо многочленов
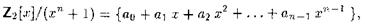 (1)
(1)
Элементами кольца являются всевозможные многочлены степени не выше п — 1 с коэффициентами 0,1 (остатки от деления на хп + 1). Операции над многочленами производятся по обычным правилам с заменой результата остатком от деления на хп + 1.
В виду очевидной биекции
двоичных слов и многочленов не будем их далее различать и говорить, например, так: код состоит из многочленов  ..., имея в виду соответствующие двоичные слова.
..., имея в виду соответствующие двоичные слова.
БЧХ-код определяется как совокупность всевозможных многочленов кольца (1), кратных некоторому фиксированному многочлену 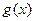 :
:
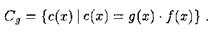
Многочлен 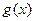 называется порождающим. Многочлен
называется порождающим. Многочлен  может быть любым, но нетрудно убедиться, что произведение
может быть любым, но нетрудно убедиться, что произведение 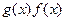 дает различные элементы кольца (1) только для многочленов
дает различные элементы кольца (1) только для многочленов  , степень (
, степень ( ) которых удовлетворяет неравенству
) которых удовлетворяет неравенству
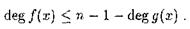
Таким образом, определение БЧХ-кода можно уточнить (1):
Порождающий многочлен 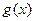 БЧХ-кода является делителем многочлена хп + 1. Многочлен
БЧХ-кода является делителем многочлена хп + 1. Многочлен 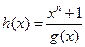 называется проверочным: код можно определить как совокупность всех таких многочленов, которые будучи умноженными на проверочный многочлен дают ноль.
называется проверочным: код можно определить как совокупность всех таких многочленов, которые будучи умноженными на проверочный многочлен дают ноль.
Корректирующие возможности БЧХ-кода определяются корнями порождающего многочлена. Так как 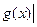 хп + 1, то корнями порождающего многочлена являются так называемые корни п-й степени из единицы, то есть элементы
хп + 1, то корнями порождающего многочлена являются так называемые корни п-й степени из единицы, то есть элементы  такие, что
такие, что 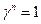 . Корни
. Корни 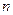 -й степени из единицы имеются в некотором поле, так как для каждого многочлена можно построить поле его разложения. Среди корней
-й степени из единицы имеются в некотором поле, так как для каждого многочлена можно построить поле его разложения. Среди корней 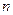 -й степени из единицы имеется примитивный
-й степени из единицы имеется примитивный 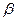 , его степени
, его степени
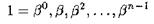
все различны и дают все решения уравнения хп — 1.
Основная теорема о БЧХ-кодах: если корнями порождающего многочлена 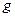 являются элементы
являются элементы
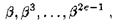
то БЧХ-код 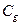 будет исправлять е ошибок.
будет исправлять е ошибок.
Возвращаемся к решению задачи. Построение кода разбивается на ряд этапов.
1. Определение поля, содержащего корни 23-й степени из 1.
Предварительно определяется мультипликативный порядок числа 2 по модулю 23. Имеем по модулю 23:
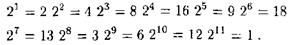
То, что 211 = 1  23 означает, что 23
23 означает, что 23 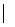
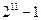 . Действительно,
. Действительно, 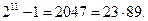
Рассмотрим поле 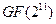 . Его можно построить как
. Его можно построить как  , где
, где  - корень неприводимого многочлена 11-й степени. Им является многочлен
- корень неприводимого многочлена 11-й степени. Им является многочлен  . Итак, если поле определить как
. Итак, если поле определить как  ,
,  , то
, то  будет примитивным элементом поля, то есть иметь 2047-й порядок.
будет примитивным элементом поля, то есть иметь 2047-й порядок.
Рассмотрим в построенном поле элемент 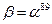 . Имеем
. Имеем 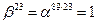 . Следовательно,
. Следовательно, 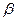 - корень 23-й степени из единицы, причем примитивный, что следует из примитивности
- корень 23-й степени из единицы, причем примитивный, что следует из примитивности  .
.

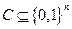 . Различаются коды по двум их основным характеристикам:
. Различаются коды по двум их основным характеристикам: , этот параметр определяет скорость передачи информации по каналу связи: если канал передает 1 бит за единицу времени, то кодированную информацию канал будет передавать с меньшей скоростью
, этот параметр определяет скорость передачи информации по каналу связи: если канал передает 1 бит за единицу времени, то кодированную информацию канал будет передавать с меньшей скоростью 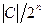 бит за единицу времени.
бит за единицу времени.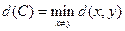 — кодовое расстояние, этот параметр определяет возможности исправления ошибок кодом С: если
— кодовое расстояние, этот параметр определяет возможности исправления ошибок кодом С: если  (С) > 2е, то код исправляет е ошибок.
(С) > 2е, то код исправляет е ошибок.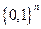 вводят различные алгебраические структуры: с их помощью дается описание кода и исследуются его параметры.
вводят различные алгебраические структуры: с их помощью дается описание кода и исследуются его параметры.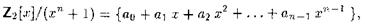 (1)
(1)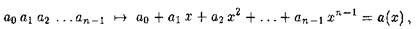
 ..., имея в виду соответствующие двоичные слова.
..., имея в виду соответствующие двоичные слова.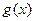 :
: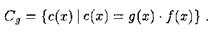
 может быть любым, но нетрудно убедиться, что произведение
может быть любым, но нетрудно убедиться, что произведение 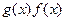 дает различные элементы кольца (1) только для многочленов
дает различные элементы кольца (1) только для многочленов  ) которых удовлетворяет неравенству
) которых удовлетворяет неравенству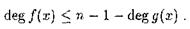
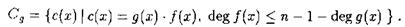
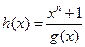 называется проверочным: код можно определить как совокупность всех таких многочленов, которые будучи умноженными на проверочный многочлен дают ноль.
называется проверочным: код можно определить как совокупность всех таких многочленов, которые будучи умноженными на проверочный многочлен дают ноль.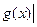 хп + 1, то корнями порождающего многочлена являются так называемые корни п-й степени из единицы, то есть элементы
хп + 1, то корнями порождающего многочлена являются так называемые корни п-й степени из единицы, то есть элементы  такие, что
такие, что 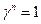 . Корни
. Корни 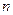 -й степени из единицы имеются в некотором поле, так как для каждого многочлена можно построить поле его разложения. Среди корней
-й степени из единицы имеются в некотором поле, так как для каждого многочлена можно построить поле его разложения. Среди корней 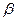 , его степени
, его степени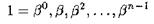
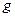 являются элементы
являются элементы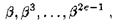
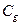 будет исправлять е ошибок.
будет исправлять е ошибок.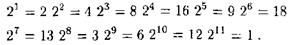
 23 означает, что 23
23 означает, что 23 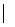
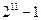 . Действительно,
. Действительно, 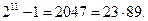
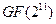 . Его можно построить как
. Его можно построить как  , где
, где  - корень неприводимого многочлена 11-й степени. Им является многочлен
- корень неприводимого многочлена 11-й степени. Им является многочлен  . Итак, если поле определить как
. Итак, если поле определить как  , то
, то 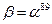 . Имеем
. Имеем 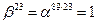 . Следовательно,
. Следовательно, 


