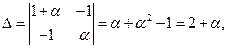Решение. Поле состоит из 25 элементов вида , где и - элементы
Поле состоит из 25 элементов вида 1) Согласно главной структурной теореме в каждом конечном поле имеется примитивный элемент, степени которого дают все ненулевые элементы поля. Этот элемент, таким образом, имеет мультипликативный порядок, равный 24; наоборот, любой элемент 24-го порядка является примитивным. Порядки остальных элементов являются делителями 24, то есть могут равняться Элемент
Отсюда следует, что Эффективного способа отыскания в конечном поле примитивного элемента не известно. Приходится перебирать элементы, выясняя их порядок. Рассмотрим, например, элемент
то есть
2) Порядок элемента элементы 1-го порядка: элементы 2-го порядка: элементы 3-го порядка: элементы 4-го порядка: элементы 6-го порядка: элементы 8-го порядка: элементы 12-го порядка: элементы 24-го порядка:
3) Минимальным многочленомэлемента конечного поля характеристики р называется многочлен наименьшей степени Для решения задачи используются два факта из теории: 1. Степени веприводимых делителей многочлена 2. Если элемент В данной задаче n = 2, поэтому все минимальные многочлены имеют первую или вторую степень; р = 5, поэтому, если элемент является корнем многочлена, то и пятая степень элемента также является корнем того же многочлена. Для элементов -2, -1, 0,1,2, входящих в простое подполе
Для вычислений используем таблицу нашего поля из решения 1). Например, для отыскания минимального многочлена элемента
4) Решить систему
Найдем решение по правилу Крамера, используя для вычислений таблицу поля Имеем
Чтобы выполнить деление, представим операнды как степени примитивного элемента
|

 , где
, где  и
и 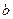 - элементы
- элементы  . Эти элементы складываются и умножаются как многочлены от
. Эти элементы складываются и умножаются как многочлены от  , при умножении
, при умножении  заменяется на
заменяется на  .
.
 . Имеем
. Имеем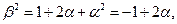

 Пусть порядок
Пусть порядок  Так как
Так как  , то
, то  то есть
то есть 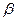 - примитивный элемент. В таблице ненулевые элементы выражены как степени
- примитивный элемент. В таблице ненулевые элементы выражены как степени 
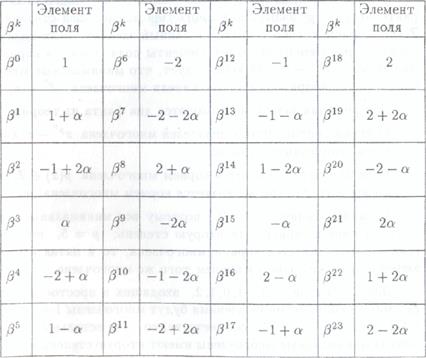
 равен
равен  . Отсюда находим
. Отсюда находим ;
; ;
; ;
; ;
; ;
; ;
; ;
;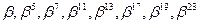 .
. , корнем которого является данный элемент. Если поле с стоит из
, корнем которого является данный элемент. Если поле с стоит из  элементов, то все элементы поля являются корня ми многочлена
элементов, то все элементы поля являются корня ми многочлена  . Отсюда следует, что минимальные многочлены - это неприводимые множители многочлена
. Отсюда следует, что минимальные многочлены - это неприводимые множители многочлена  является корнем многочлена
является корнем многочлена  ,то элемент
,то элемент  также является корнем многочлена
также является корнем многочлена  ).
). , минимальными многочленами будут многочлены 1-й степени х + 2, х + 1, х, х - 1, х - 2, соответственно. Для остальных 20 элементов минимальные многочлены имеют вторую степень и могут быть вычислены следующим образом. Пусть требуется найти минимальный многочлен
, минимальными многочленами будут многочлены 1-й степени х + 2, х + 1, х, х - 1, х - 2, соответственно. Для остальных 20 элементов минимальные многочлены имеют вторую степень и могут быть вычислены следующим образом. Пусть требуется найти минимальный многочлен  элемента
элемента  , отсюда по формулам Виета
, отсюда по формулам Виета
 . По таблице находим
. По таблице находим
 Следовательно, минимальный многочлен равен
Следовательно, минимальный многочлен равен  Вычисления сведем в таблицу.
Вычисления сведем в таблицу.

 , построенную выше при решении пункта 1).
, построенную выше при решении пункта 1).