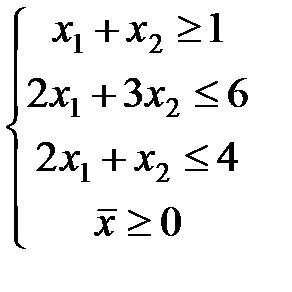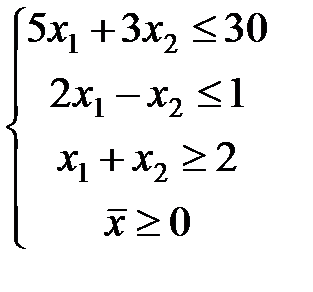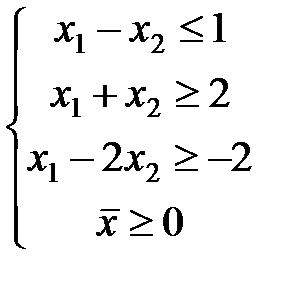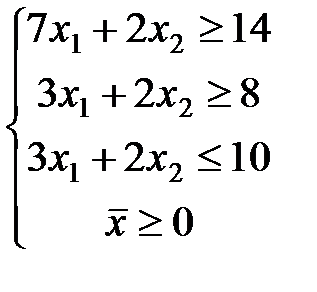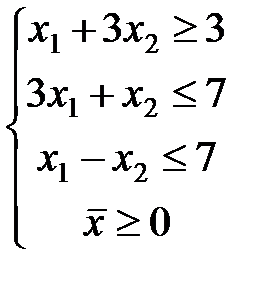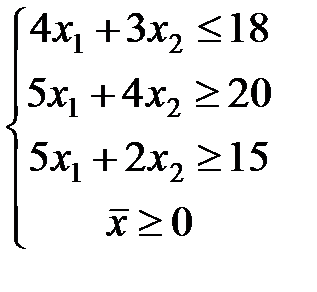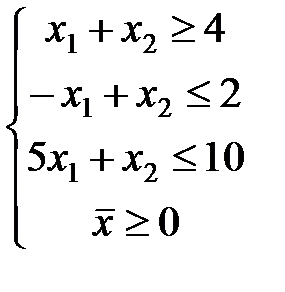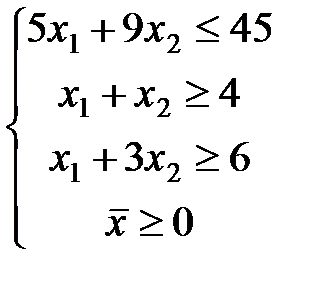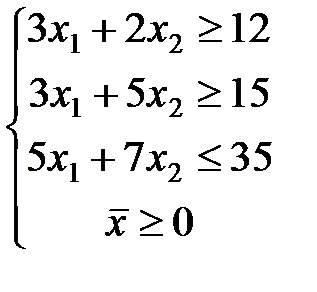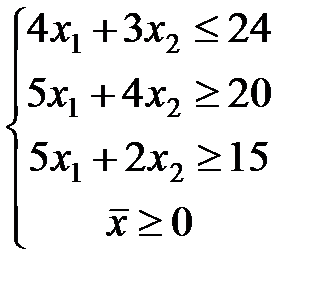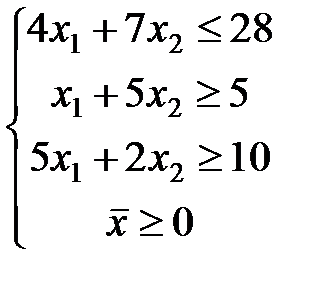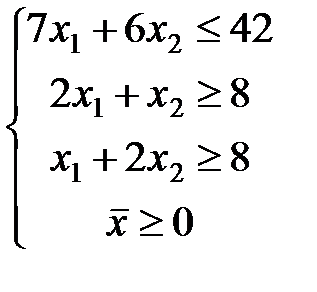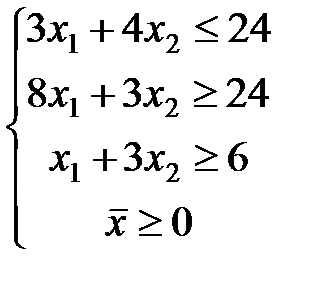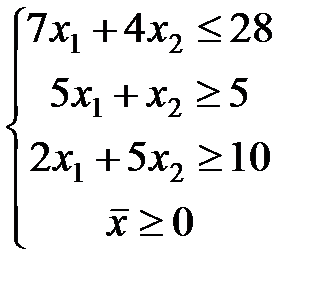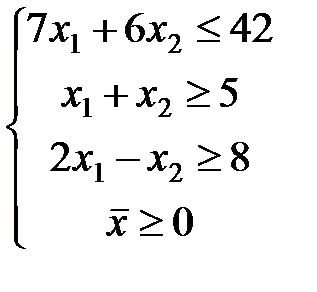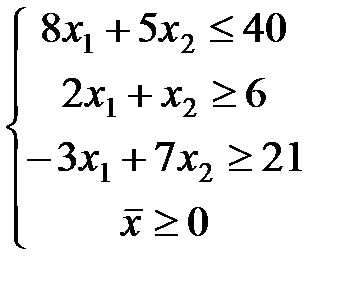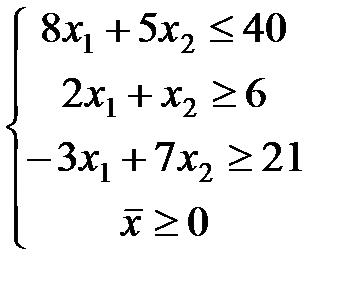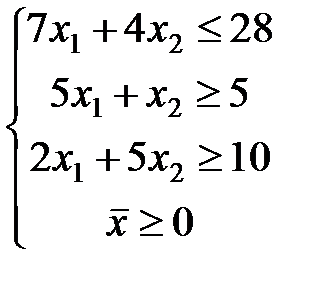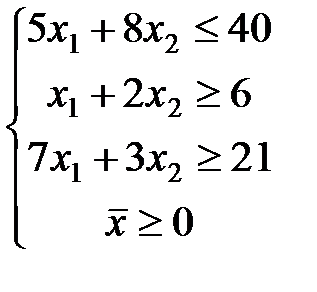Даны векторы  ,
,  , угол между векторами
, угол между векторами  и
и 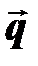 равен
равен  .
.
Вычислить: 1) длины диагоналей параллелограмма, построенного на векторах 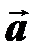 и
и 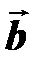 ; 2) острый угол между диагоналями параллелограмма; 3) площадь параллелограмма.
; 2) острый угол между диагоналями параллелограмма; 3) площадь параллелограмма.
Значения коэффициентов l, m, n, k, f и модули векторов 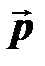 и
и 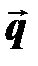 даны ниже для каждого варианта.
даны ниже для каждого варианта.
ЗАДАЧА № 2
Даны координаты вершин пирамиды A1A2A3A4: A1(x1 ; y1 ; z1), A2(x2 ; y2 ; z2), A3(x3 ; y3 ; z3), A4(x4 ; y4 ; z4).
Требуется: 1) в декартовой прямоугольной системе координат построить пирамиду A1A2A3A4; 2) записать векторы 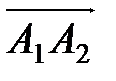 ,
,  ,
, 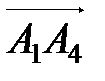 в ортонормированном базисе и найти модули этих векторов; 3) найти острый угол между векторами
в ортонормированном базисе и найти модули этих векторов; 3) найти острый угол между векторами 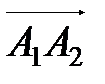 и
и 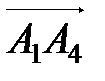 ; 4) найти площадь треугольника A1A2A3; 5) найти объем пирамиды A1A2A3A4.
; 4) найти площадь треугольника A1A2A3; 5) найти объем пирамиды A1A2A3A4.
| Вариант
| 
| 
| 
| 
|
|
| (2; 3; 2)
| (10; 7; 3)
| (6; 6; 3)
| (8; 9; 5)
|
|
| (3; 5; 2)
| (1; 7; 5)
| (5; 6; 8)
| (1; 6; 4)
|
|
| (6; 1; 4)
| (3;-3; 8)
| (5;-5; 8)
| (8; 3; 3)
|
|
| (2; 5; 4)
| (5; 3; 6)
| (8; 3; 5)
| (8; 2; 10)
|
|
| (3; 4; 3)
| (7;-4; 4)
| (6; 0; 4)
| (9; 10; 6)
|
|
| (1; 2; 3)
| (3; 4; 6)
| (-3; 1; 6)
| (3; 3; 5)
|
|
| (3; 5; 1)
| (0; 1; 5)
| (1; 0; 5)
| (7; 9;-1)
|
|
| (5;-2; 4)
| (7; 1; 6)
| (7; 4; 5)
| (8; 4; 10)
|
|
| (1; 2; 1)
| (9;-2; 2)
| (-3; 5; 0)
| (7; 8;-2)
|
|
| (4; 1; 3)
| (2; 3; 6)
| (5;-3; 6)
| (3; 3; 5)
|
|
| (3;-1; 2)
| (7; 2; 6)
| (9; 0; 6)
| (5; 1; 3)
|
|
| (3; 5; 4)
| (1; 8; 6)
| (-1; 2; 6)
| (9;-1; 1)
|
|
| (1; 1; 2)
| (-3; 9; 3)
| (-2; 5; 3)
| (7; 7;-1)
|
|
| (1; 4; 3)
| (-1; 6; 6)
| (6;-4; 0)
| (2; 2; 1)
|
| Вариант
| 
| 
| 
| 
|
|
| (2; 4; 1)
| (6; 7; 5)
| (7; 6; 5)
| (6; 8; 3)
|
|
| (1; 2; 2)
| (3; 5; 4)
| (5;-1; 4)
| (7; 8; 5)
|
|
| (2;-2; 1)
| (10; 2; 2)
| (6; 1; 2)
| (8; 4; 4)
|
|
| (3; 4;-1)
| (1; 6; 2)
| (5; 5; 5)
| (1; 5; 1)
|
|
| (2; 5; 3)
| (-1; 1; 7)
| (1;-1; 7)
| (4; 7; 2)
|
|
| (1; 4; 2)
| (4; 2; 4)
| (7; 2; 3)
| (7; 1; 8)
|
|
| (3; 1; 4)
| (7;-7; 5)
| (6;-3; 5)
| (9; 7; 7)
|
|
| (2; 4; 3)
| (4; 6; 6)
| (-2; 3; 6)
| (4; 5; 5)
|
|
| (5;-2;-1)
| (2;-6; 3)
| (3;-7; 3)
| (9; 2;-3)
|
|
| (5; 2; 1)
| (7; 5; 3)
| (7; 8; 2)
| (8; 8; 7)
|
|
| (2;-1; 7)
| (10;-5; 8)
| (-2; 2; 6)
| (8; 5; 4)
|
|
| (4; 7; 8)
| (2; 9; 11)
| (5; 3; 11)
| (3; 9; 10)
|
|
| (2; 1; 3)
| (6; 4; 7)
| (8; 2; 7)
| (4; 3; 4)
|
|
| (1; 5; 2)
| (-1; 8; 4)
| (-3; 2; 4)
| (7;-1;-1)
|
|
| (6; 1; 4)
| (2; 9; 5)
| (3; 5; 5)
| (12; 7; 1)
|
|
| (6; 5; 1)
| (4; 7; 4)
| (11;-3;-2)
| (7; 3;-1)
|
ЗАДАЧА № 3
Построить кривую, заданную уравнением в полярной системе координат.
| Вариант
| Уравнение кривой
| Вариант
| Уравнение кривой
| |
|
| r =  + 2cos 2j + 2cos 2j
|
| r = 3 – 3sin 2j
| |
|
| r = 3 + sin 2j
|
| r =  – 2cos 2j – 2cos 2j
| |
|
| r =  – 2cos 3j – 2cos 3j
|
| r = 3 – sin 2j
| |
|
| r = 2 – 2sin 3j
|
| r =  + 2cos 3j + 2cos 3j
| |
|
| r =  + 2sin 3j + 2sin 3j
|
| r = 2 + 2sin 3j
| |
|
| r = 4 + 2cos 3j
|
| r =  – 2sin 3j – 2sin 3j
| |
|
| r =  – 2sin 2j – 2sin 2j
|
| r = 4 – 2cos 3j
| |
|
| r = 3 – 3cos 2j
|
| r =  + 2sin 2j + 2sin 2j
| |
|
| r =  + 2sin 2j + 2sin 2j
|
| r = 3 + 3cos 2j
| |
|
| r = 3 + cos 2j
|
| r =  – 2sin 2j – 2sin 2j
| |
|
| r =  – 2sin 3j – 2sin 3j
|
| r = 3 – cos 2j
| |
| Вариант
| Уравнение кривой
|
| Уравнение кривой
|
|
| r = 2 – 2cos 3j
|
| r =  + 2sin 3j + 2sin 3j
|
|
| r =  + 2cos 3j + 2cos 3j
|
| r = 2 + 2cos 3j
|
|
| r = 4 + 2sin 3j
|
| r =  – 2cos 3j – 2cos 3j
|
|
| r =  – 2cos 2j – 2cos 2j
|
| r = 4 – 2sin 3j
|
| | | | | | |
ЗАДАЧА № 4
Решить графически систему линейных неравенств.

 ,
,  , угол между векторами
, угол между векторами  и
и 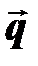 равен
равен  .
.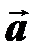 и
и 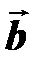 ; 2) острый угол между диагоналями параллелограмма; 3) площадь параллелограмма.
; 2) острый угол между диагоналями параллелограмма; 3) площадь параллелограмма.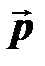 и
и 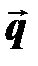 даны ниже для каждого варианта.
даны ниже для каждого варианта.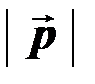


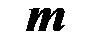
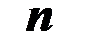
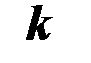

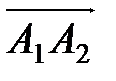 ,
,  ,
, 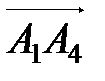 в ортонормированном базисе и найти модули этих векторов; 3) найти острый угол между векторами
в ортонормированном базисе и найти модули этих векторов; 3) найти острый угол между векторами 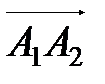 и
и 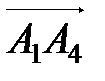 ; 4) найти площадь треугольника A1A2A3; 5) найти объем пирамиды A1A2A3A4.
; 4) найти площадь треугольника A1A2A3; 5) найти объем пирамиды A1A2A3A4.



 + 2cos 2j
+ 2cos 2j
 – 2cos 3j
– 2cos 3j