Решить графически систему линейных неравенств
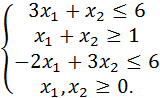
Решение
1. Построим прямые (рис.1):
1) 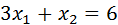 ; 2)
; 2) 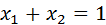 ; 3)
; 3) 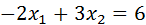 .
.
| х 1
|
|
|
| х 1
|
|
|
| х 1
|
| -3
|
| х 2
|
|
|
| х 2
|
|
|
| х 2
|
|
|
2. Для каждой прямой определим полуплоскость, которая задается неравенством. Для этого возьмем произвольную точку, не лежащую на прямой, и подставим ее координаты в неравенство. Если неравенство будет верным, то полуплоскость, содержащая выбранную точку, и является решением исходного неравенства. Если неравенство будет неверным, то решением неравенства будет полуплоскость по другую сторону прямой.
1) Возьмем, например, точку О(0;0): 3×0+0£6 (верно), значит решением неравенства будет полуплоскость, содержащая эту точку.
2) Возьмем точку О(0;0) и подставим ее координаты во второе неравенство: 0+0³1 (неверно). Значит, решением неравенства является полуплоскость, не содержащая точку О.
3) Выберем, например, точку О(0;0) и подставим ее координаты в третье неравенство: -2×0+3×0£6 (верно). Значит, решением неравенства является полуплоскость, содержащая точку О.
3. Решением системы неравенств будет область пересечения всех полуплоскостей, являющихся решением каждого из неравенств системы. В данном примере решением системы является область АВСDEFG. Так как по условию х 1>0 и x 2>0, то области АВС и EFG исключаются из решения. Таким образом, получаем область АСDEG, в которой координаты всех точек, кроме D известны. Найдем координаты точки D. Необходимо решить систему уравнений:
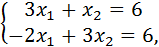
ее решением будет т.  .
.
Ответ: АСDEG – область решений системы.

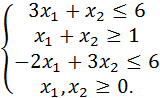
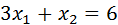 ; 2)
; 2) 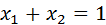 ; 3)
; 3) 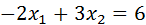 .
.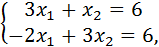
 .
.


