Контрольная работа №1. А) построить пирамиду АВСD
1. Даны координаты вершин пирамиды АВСD. А(2;2;2) В(4;3;3) С(4;5;4) D(5;5;6.) а) построить пирамиду АВСD; б) найти ее объем VABCD; в) найти площадь DABC SDABC; г) найти cos(ABÙAC); д) найти прADAC. Ответ: б) д) 2. Найти площадь треугольника, построенного на векторах
Ответ: Найти длину вектора Ответ: Контрольная работа №2 1. Даны координаты точек А(2; 2); В(-2; -8); М(-6; -2). а) написать общее уравнение прямой (АВ); б) найти расстояние от точки М до прямой (АВ); в) написать уравнения прямых, проходящих через точку М параллельно и перпендикулярно прямой (АВ). Ответ: а) 5х-2у-6=0; б) 2. Написать уравнение прямой, проходящей через левый фокус кривой Ответ: 3х-2у+12=0. 3. Даны координаты точек А(2; 3; 3); В(1; 1; 1); С(3; 3; 2). а) написать параметрические и канонические уравнения прямой (АВ); б) написать уравнение прямой, проходящей через точку С параллельно прямой (АВ); в) написать общее уравнение плоскости АВС; г) найти расстояние начала координат до плоскости АВС; д) найти угол между прямой (АО) и плоскостью АВС; е) найти проекцию точки О на плоскость АВС. Ответ: а) в) 2х-3у+2z-1 =0; г) ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ К ЭКЗАМЕНУ
1.Векторы: длина и направление, коллинеарность и компланарность. Равенство векторов. 2.Линейные операции над векторами и их свойства. 3.Линейное векторное пространство. 4. Линейная зависимость и независимость. Теоремы о линейной зависимости. 5.Геометрический смысл линейной зависимости на плоскости и в трехмерном пространстве. 6.Базис и система координат. Единственность разложения вектора по базису. Теоремы о координатах суммы векторов и произведении вектора на число. 7.Преобразование координат вектора при смене базиса. 8.Аффинные пространства. Аффинные системы координат. 9.Проекция вектора на ось. Теоремы о проекции вектора на ось. 10.Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты сомножителей. 11.Евклидовы, нормированные и метрические пространства. Неравенства Коши - Буняковского и треугольника. 12.Векторное произведение векторов и его свойства. Выражение векторного произведения через координаты сомножителей. 13.Смешанное произведение векторов и его свойства. Выражение смешанного произведения через координаты сомножителей. 14.Двойное векторное произведение. Условия ассоциативности векторного произведения. 15.Деление отрезка в заданном отношении. 16.Полярные и обобщенные полярные координаты на плоскости. 17.Цилиндрическая и сферическая системы координат. 18.Различные виды уравнений прямой на плоскости. 19.Угол между прямыми. Условия параллельности и перпендикулярности прямых на плоскости. Расстояние от точки до прямой. 20.Геометрический смысл неравенств первого порядка. 21.Различные виды уравнений плоскости в пространстве. 22.Угол между плоскостями, условия параллельности и перпендикулярности плоскостей. Расстояние от точки до плоскости. 23.Различные виды уравнений прямой в пространстве. Расстояние от точки до прямой в пространстве. 24.Взаимное расположение прямых в пространстве. 25.Взаимное расположение прямых и плоскостей в пространстве. 26.Эллипс. 27.Гипербола. 28.Парабола. 29.Оптические свойства эллипса, гиперболы и параболы. 30.Упрощение общего уравнения линии второго порядка при параллельном переносе. 31.Упрощение общего уравнения линии второго порядка при повороте осей координат. 32.Классификация кривых второго порядка. 33.Основные поверхности второго порядка: сфера, эллипсоид, гиперболоиды и параболоиды. 34.Цилиндрические поверхности. 35.Конические поверхности. 36.Классификация поверхностей второго порядка. 37.Инварианты общего уравнения кривой второго порядка. 38.Инварианты общего уравнения поверхности второго порядка.
Примерные варианты экзаменационных билетов (практическая часть) Вариант 001
1. Найдите 2. Найдите площадь треугольника, построенного на векторах 3. Даны точки А(4;2;5); В(0;7;1), С(0;2;7); Д(1;5;0). а) найдите SDАВС; б) найдите объем пирамиды АВСД. 4.. Напишите уравнение прямой, проходящей через правый фокус линии 16 х 2+25 у 2=400 и ее нижнюю вершину. 5.. Напишите канонические уравнения прямой, проходящей через точку М(5;4;2) параллельно прямой 6. Назовите поверхность, заданную уравнением
Вариант 002
1. Какой угол образуют единичные векторы 2. Найдите площадь параллелограмма, построенного на векторах 3. Даны точки А(2;1;3); В(-2;6;7), С(-2;1;5); Д(-1;4;-2). а) найдите SDАВС; б) найдите объем пирамиды АВСД. 4. Напишите уравнение прямой, проходящей через фокус линии у 2=-4 x перпендикулярно прямой 7 х -3 у +2=0. 5. Напишите уравнение плоскости, проходящей через прямую 6. Назовите поверхность, заданную уравнением
Ответы: Вариант 001: 1) -25; 2) 5; 3) а /SD= 5) Вариант 002: 1)
Список рекомендУЕМой литературы ОСНОВНАЯ 1) учебники 1. Кузютин, В.Ф. геометрия:.учебник для вузов./ В.Ф. Кузютин, Н.А.Зенкевич, В.В. Еремеев.-СПб.:«Лань», 2003. 2. Бугров, Я.С. Высшая математика / Я.С. Бугров, С.М. Никольский. Т.1. Элементы линейной алгебры и аналитической геометрии. – М.: Дрофа, 2003. 3. Ефимов Н.В. Краткий курс аналитической геометрии / Н.В. Ефимов. – М.: Физматлит, 2002. 4. Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. − 2-е изд., испр. − М.: Айрис-пресс, 2002. – Ч. 1.
2) задачники
5. Болгов., В.А. Сборник задач по математике для втузов. Ч.1. Линейная алгебра и основы математического анализа: учеб. пособие для втузов/ В.А. Болгов., Б.П. Демидович, А.В. Ефимов и др.; под ред. А.В. Ефимова, Б.П. Демидовича. - М.: Наука, 1993. 6. Минорский, В.П. Сборник задач по высшей математике: Учеб. пособие для втузов./ В.П. Минорский. – М.: физ-мат. лит., 2004. Лунгу, К.Н. Сборник задач по высшей математике. I курс / К.Н. Лунгу, Д.Т. Письменный, С.Н. Федин, Ю.А. Шевченко. – 7-е изд.– М.: Айрис-пресс, 2008.
ДОПОЛНИТЕЛЬНАЯ 7. Ильин, В.А. Аналитическая геометрия / В.А. Ильин, Э.Г. Поздняк. – М.: Физматлит, 2006. 8. Ильин, В.А. Линейная алгебра / В.А. Ильин, Э.Г. Поздняк. - М.: Наука, 1999. 9. Данко, П.Е. Высшая математика в упражнениях и задачах / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высш. шк., 1999. – Ч. 1. 10. Клетеник, Д.В. Сборник задач по аналитической геометрии / Д.В. Клетеник. – М.: Профессия, 2006. 11. Беклемишев, Д.В. Курс аналитической геометрии и линейной алгебры./ Д.В. Беклемишев. – М.: физматлит., 2001.
|

 ; в)
; в) 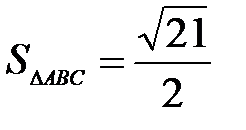 ; г)
; г) 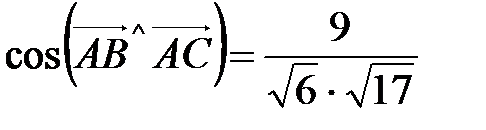 ;
;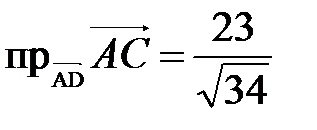 .
. .
. .
.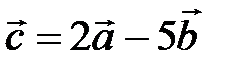 , если
, если 
 .
. ; в) 5х-2у+26=0; 2х+5у+22=0.
; в) 5х-2у+26=0; 2х+5у+22=0. параллельно прямой 3x-2y+1=0. Построить прямую и кривую.
параллельно прямой 3x-2y+1=0. Построить прямую и кривую. ;
;  ; б)
; б)  ;
; ; д)
; д) 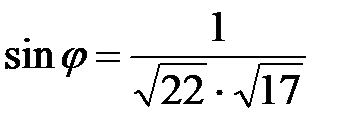 ; е)
; е)  .
. , если
, если  .
. , если
, если 

 , если известно, что векторы
, если известно, что векторы  ортогональны?
ортогональны? , если
, если  и угол между ними α = 60º
и угол между ними α = 60º  .
. перпендикулярно плоскости х +4 у -3 z +7=0.
перпендикулярно плоскости х +4 у -3 z +7=0. ; б) V=29/3; 4) 4х-3у-12=0;
; б) V=29/3; 4) 4х-3у-12=0; ; 6) однополосный гиперболоид, ось Оу.
; 6) однополосный гиперболоид, ось Оу. 2) 51; 3) а /SD=
2) 51; 3) а /SD=  ; б) V=77/3; 4)3x+7y+3=0; 5) 4x-7y-8z+25=0; 6) гиперболический параболоид, ось Оу.
; б) V=77/3; 4)3x+7y+3=0; 5) 4x-7y-8z+25=0; 6) гиперболический параболоид, ось Оу.


