Даны координаты вершин треугольника 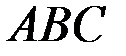 :
: 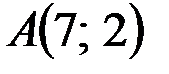 ,
,  ,
,  . Найти: 1) длину стороны
. Найти: 1) длину стороны  ; 2) уравнения сторон
; 2) уравнения сторон  и
и  и их угловые коэффициенты; 3) внутренний угол
и их угловые коэффициенты; 3) внутренний угол  в радианах с точностью до
в радианах с точностью до  ; 4) уравнение высоты
; 4) уравнение высоты  и ее длину, не используя координаты точки
и ее длину, не используя координаты точки 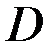 ; 5) уравнение медианы
; 5) уравнение медианы  ; 6) точку пересечения высот треугольника
; 6) точку пересечения высот треугольника  . Сделать чертеж.
. Сделать чертеж.
Решение: Сделаем чертеж (рис.3).
Рис. 3
1. Расстояние между точками  и
и  находится по формуле
находится по формуле  .
.
В данном случае  .
.
2. Уравнение прямой, проходящей через две заданные точки плоскости  и
и  имеет вид
имеет вид  .
.
Следовательно, для прямой  имеем
имеем 

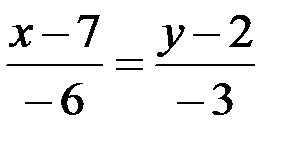
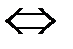
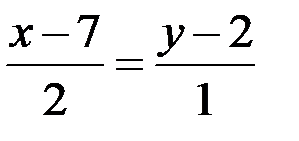
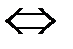
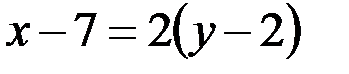
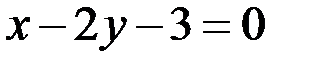 – общее уравнение прямой
– общее уравнение прямой  .
.
Аналогично, для прямой  имеем
имеем 





 – общее уравнение прямой
– общее уравнение прямой  .
.
Найдем угловые коэффициенты прямых 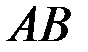 и
и 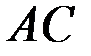 . Для этого перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом
. Для этого перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом  .
.
Для прямой  имеем
имеем  , то есть
, то есть  – угловой коэффициент прямой
– угловой коэффициент прямой 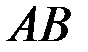 . Для прямой
. Для прямой  получим
получим  , значит
, значит  – угловой коэффициент прямой
– угловой коэффициент прямой 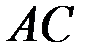 .
.
3. Учитывая, что угол  острый, воспользуемся формулой
острый, воспользуемся формулой  .
.
Имеем  , откуда
, откуда 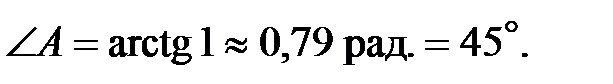
4. Для нахождения уравнения высоты 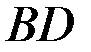 воспользуемся формулой уравнения прямой, проходящей через данную точку
воспользуемся формулой уравнения прямой, проходящей через данную точку  с заданным угловым коэффициентом
с заданным угловым коэффициентом  :
:  .
.
В данном случае  ;
;  (координаты точки
(координаты точки  ). Так как прямые
). Так как прямые  и
и  перпендикулярны, то их угловые коэффициенты связаны соотношением
перпендикулярны, то их угловые коэффициенты связаны соотношением  , откуда
, откуда  . Значит, уравнение высоты
. Значит, уравнение высоты  будет иметь вид:
будет иметь вид:  или
или  .
.
Для нахождения длины высоты  воспользуемся формулой расстояния
воспользуемся формулой расстояния  от заданной точки
от заданной точки  до прямой
до прямой  :
:  .
.
В данном случае 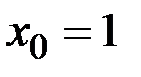 ,
,  (координаты точки
(координаты точки  );
);  ;
; 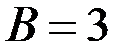 ;
; 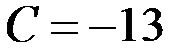 (коэффициенты из общего уравнения прямой
(коэффициенты из общего уравнения прямой  ). Следовательно,
). Следовательно,  .
.
5. Уравнение медианы  составим, используя уравнение прямой, проходящей через две заданные точки.
составим, используя уравнение прямой, проходящей через две заданные точки.
Так как 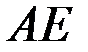 – медиана, то координаты точки
– медиана, то координаты точки  найдем как координаты середины отрезка
найдем как координаты середины отрезка  :
:  ;
;  , то есть
, то есть  . Тогда уравнение медианы
. Тогда уравнение медианы  будет иметь вид:
будет иметь вид:  или
или 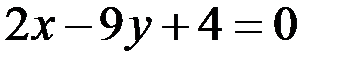 .
.
6. Для нахождения координат точки  пересечения высот треугольника
пересечения высот треугольника  найдем уравнение высоты
найдем уравнение высоты  .
.
Уравнение высоты  находим по формуле
находим по формуле  . По условию
. По условию 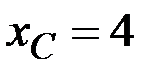 ,
,  . Так как прямые
. Так как прямые  и
и  перпендикулярны, то
перпендикулярны, то 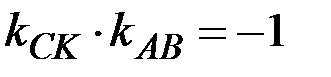 ;
;  . Значит, уравнение высоты
. Значит, уравнение высоты  будет иметь вид
будет иметь вид 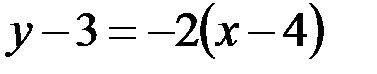 или
или 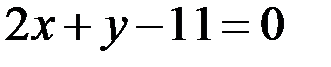 .
.
Составляем и решаем систему уравнений: 

 Значит,
Значит,  .
.

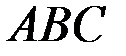 :
: 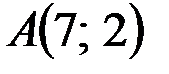 ,
,  ,
,  . Найти: 1) длину стороны
. Найти: 1) длину стороны  ; 2) уравнения сторон
; 2) уравнения сторон  и
и  и их угловые коэффициенты; 3) внутренний угол
и их угловые коэффициенты; 3) внутренний угол  в радианах с точностью до
в радианах с точностью до  ; 4) уравнение высоты
; 4) уравнение высоты  и ее длину, не используя координаты точки
и ее длину, не используя координаты точки 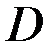 ; 5) уравнение медианы
; 5) уравнение медианы  ; 6) точку пересечения высот треугольника
; 6) точку пересечения высот треугольника  . Сделать чертеж.
. Сделать чертеж. и
и  находится по формуле
находится по формуле  .
. .
. и
и  имеет вид
имеет вид  .
. имеем
имеем 

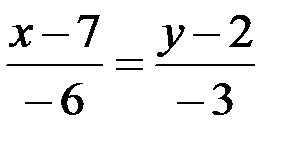
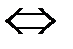
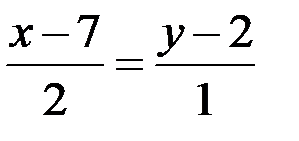
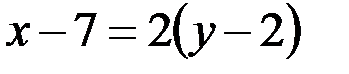
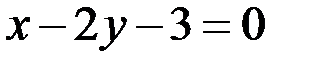 – общее уравнение прямой
– общее уравнение прямой  имеем
имеем 


 – общее уравнение прямой
– общее уравнение прямой  .
.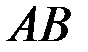 и
и 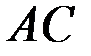 . Для этого перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом
. Для этого перейдем от общего уравнения прямой к уравнению прямой с угловым коэффициентом  .
. имеем
имеем  , то есть
, то есть  – угловой коэффициент прямой
– угловой коэффициент прямой  получим
получим  , значит
, значит  – угловой коэффициент прямой
– угловой коэффициент прямой 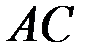 .
. острый, воспользуемся формулой
острый, воспользуемся формулой  .
. , откуда
, откуда 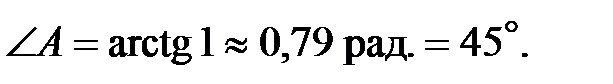
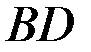 воспользуемся формулой уравнения прямой, проходящей через данную точку
воспользуемся формулой уравнения прямой, проходящей через данную точку  с заданным угловым коэффициентом
с заданным угловым коэффициентом  :
:  .
. ;
;  (координаты точки
(координаты точки  ). Так как прямые
). Так как прямые  и
и  перпендикулярны, то их угловые коэффициенты связаны соотношением
перпендикулярны, то их угловые коэффициенты связаны соотношением  , откуда
, откуда  . Значит, уравнение высоты
. Значит, уравнение высоты  или
или  .
. от заданной точки
от заданной точки  до прямой
до прямой  :
:  .
.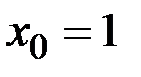 ,
,  (координаты точки
(координаты точки  );
);  ;
; 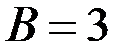 ;
; 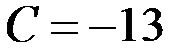 (коэффициенты из общего уравнения прямой
(коэффициенты из общего уравнения прямой  ). Следовательно,
). Следовательно,  .
. составим, используя уравнение прямой, проходящей через две заданные точки.
составим, используя уравнение прямой, проходящей через две заданные точки.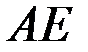 – медиана, то координаты точки
– медиана, то координаты точки  найдем как координаты середины отрезка
найдем как координаты середины отрезка  :
:  ;
;  , то есть
, то есть  . Тогда уравнение медианы
. Тогда уравнение медианы  или
или 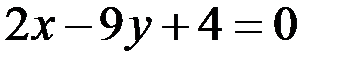 .
. пересечения высот треугольника
пересечения высот треугольника  найдем уравнение высоты
найдем уравнение высоты  .
. . По условию
. По условию 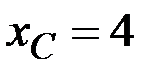 ,
,  . Так как прямые
. Так как прямые  и
и  перпендикулярны, то
перпендикулярны, то 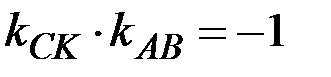 ;
;  . Значит, уравнение высоты
. Значит, уравнение высоты  будет иметь вид
будет иметь вид 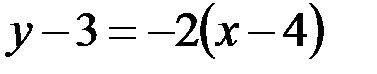 или
или 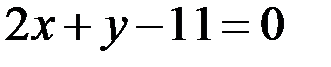 .
.

 Значит,
Значит,  .
.


