Задача 9. Решение. Поскольку для квадратичной формы а 11х2+а 22у2+а 33z2+2a 12xy+2a 13xz+2a 23yz матрица имеет вид
Привести к каноническому виду уравнение поверхности второго порядка 3х2+3у2-2yz+3z2-1=0 с помощью теории квадратичных форм. Сделать чертеж поверхности в канонической системе координат. Решение. Поскольку для квадратичной формы а 11х2+ а 22у2+ а 33z2+2 a 12xy+2 a 13xz+2 a 23yz матрица имеет вид
то в нашем примере матрица старших членов уравнения поверхности имеет вид
Найдем собственные значения этой матрицы. Для этого составим и решим характеристическое уравнение
которое приводится к виду (3-l)3-(3-l)=0 или (3-l)(l2-6l+8)=0. Отсюда находим l1=3, l2=2, l3=4. Найдем собственные векторы для каждого собственного значения. Пусть
При l1=3 получаем систему
Следовательно, в системе 2 главные неизвестные, 1 свободная. Пусть х 1- свободная неизвестная, придадим ей значение 1, т.е. х 1=1. Тогда получаем При l2=2 получаем систему
Следовательно, в системе две главные неизвестные, одна свободная. Пусть х 3 – свободная неизвестная, придадим ей значение 1, т.е. х 3=1. Тогда получаем систему Значит, При l3=4 получаем систему
Следовательно, в системе две главные неизвестные, одна свободная. Пусть х 3 – свободная неизвестная, придадим ей значение 1, т.е. х 3=1. Тогда получаем систему Значит, Пронормируем собственные векторы.
Запишем матрицу преобразования координат
Отсюда получаем формулы преобразования координат x=x'; y= z= Значения х,у,z подставим в исходное уравнение поверхности
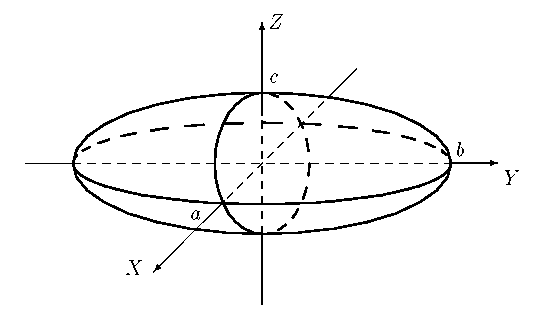
или 3x'2+2y'2+4z'2-1=0. Заметим, что коэффициенты x'2, у'2, z'2, как и должно было быть, являются соответственно собственными значениями l1, l2, l3. Таким образом, получили уравнение поверхности 3x'2+2y'2+4z'2=1 или
Рис. 8
Примерные варианты контрольных работ
|



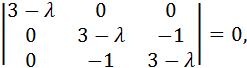
 – собственный вектор. Координаты собственных векторов являются решениями системы (А-lЕ)
– собственный вектор. Координаты собственных векторов являются решениями системы (А-lЕ)  . В нашем случае эта система имеет вид
. В нашем случае эта система имеет вид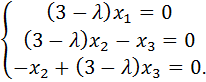

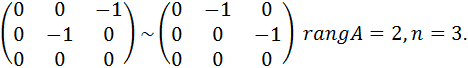
 собственный вектор для собственного значения l1=3.
собственный вектор для собственного значения l1=3.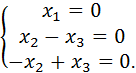


 собственный вектор для собственного значения l2=2.
собственный вектор для собственного значения l2=2.

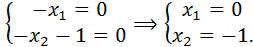
 собственный вектор для собственного значения l3=4.
собственный вектор для собственного значения l3=4.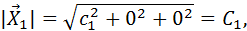 следовательно,
следовательно, 
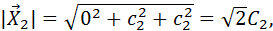 следовательно,
следовательно, 
 следовательно,
следовательно, 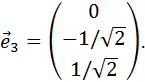

 y'-
y'- 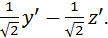

 эллипсоид (рис.8).
эллипсоид (рис.8).