Анализ вида напорной характеристики и характеристики КПД турбокомпрессора
Как указывалось выше, особенностью газодинамических характеристик турбокомпрессоров является наличие в них точек максимума, левее и правее которых напор (давление, удельная работа) или КПД снижаются. Этот максимум может быть либо явно выражен, либо иметь размытый характер. Характеристика теоретического напора, как было показано в гл. 6, представляет собой прямую линию, которая в зависимости от угла βл 2, может быть возрастающей, убывающей или параллельной оси абсцисс (φ;2). Это следует из формулы
Для РК с конечным числом лопаток линейность характеристики сохраняется
Проанализируем причины, приводящие к тому, что действительные характеристики турбокомпрессоров отличаются от теоретических на примере характеристик В уравнении Бернулли
будем считать, что гидравлические потери напора в РК hw состоят из потерь на трение в проточной части hwтр и ударных потерь hwуд, обусловленных наличием углов атаки при входе на лопатки рабочего колеса( Тогда
или в безразмерном виде
Определим потери на трение в проточной части в безразмерном виде
Потери энергии на трение можно вычислить по относительной скорости во входном сечении межлопаточного канала РК [6]
где ζ тр – коэффициент потерь на трение. Тогда, заменяя
а с учетом того, что
Предположим, что Для определения
Ударные потери можно также определить по гидравлической формуле, где в качестве характерной скорости можно принять отрезок Δ Wu (рис. 8.4):
где ζ уд – коэффициент ударных потерь. Из треугольников скоростей следует
принимая во внимание, что
Таким образом, Вычитая последовательно из зависимости Форму напорной характеристики можно объяснить следующим образом: снижение напора правее расчетного режима объясняется как самой формой зависимости коэффициента теоретического напора ψТ (прямая ψТ с увеличением φ;2 уменьшается), так и увеличением ударных потерь и потерь на трение, а форма напорной характеристики левее φ;2расч объясняются главным образом ударными потерями.
Рис. 8.5. Анализ формы характеристик
Снижение КПД вправо и влево от расчетной точки также объясняется вышеперечисленными явлениями:
Гидравлический и внутренний КПД связаны между собой через коэффициенты потерь на протечки и дисковое трение:
|

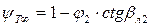 .
.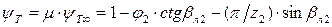 .
.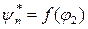 и
и 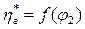 ступени с рабочим колесом имеющим угол βл 2<90° без закрутки потока на входе СU 1=0.
ступени с рабочим колесом имеющим угол βл 2<90° без закрутки потока на входе СU 1=0.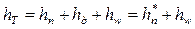
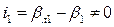 ).
).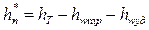 ,
,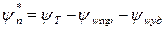 (8.3)
(8.3)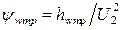 .
.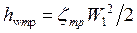 ,
, (рис. 8.4), получим
(рис. 8.4), получим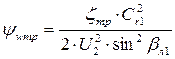 ,
, – коэффициент расхода,
– коэффициент расхода,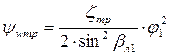 . (8.4)
. (8.4)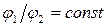 , тогда
, тогда 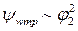 . Таким образом, функция
. Таким образом, функция 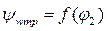 представляет собой параболу с вершиной в начале координат (при φ;2=0, ψwтр =0).
представляет собой параболу с вершиной в начале координат (при φ;2=0, ψwтр =0).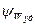 построим треугольники скоростей для двух режимов – расчетного (
построим треугольники скоростей для двух режимов – расчетного (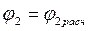 ) и нерасчетного, например
) и нерасчетного, например 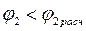 (рис. 8.4).
(рис. 8.4).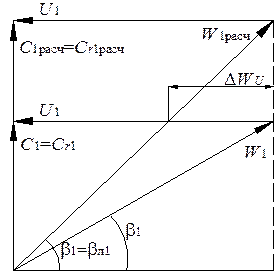 Рис. 8.4. Треугольники скоростей на входе в РК на расчетном и нерасчетном режимах
Рис. 8.4. Треугольники скоростей на входе в РК на расчетном и нерасчетном режимах
 ,
,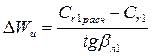 ,
,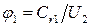 и
и 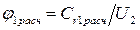 , имеем
, имеем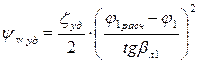 . (8.5)
. (8.5) и функция
и функция 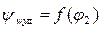 представляет собой параболу с вершиной при φ;2= φ;2расч (при i 1= 0, φ;2= φ;2расч и ψwуд =0).
представляет собой параболу с вершиной при φ;2= φ;2расч (при i 1= 0, φ;2= φ;2расч и ψwуд =0).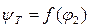 функции
функции 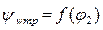 и
и  -
- 
 .
.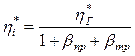 .
.


