При стабильной регуляции реакция на ступенчатое воздействие (внешнее возмущение либо изменение рабочего значения) в конечном итоге приводит к стационарному состоянию (рис. 15.4, Г и 15.5, Д). При этом управляемая переменная, обратная связь и сигналы управления перестают быть функциями времени и имеют постоянные значения. В этом состоянии элементы цепи управления могут быть описаны статическими характеристическими кривыми. В целом характеристические кривые для системы описывают соотношения между величинами на входе и на выходе. Статическая характеристика датчика (мышечного веретена) - соотношение между частотой разряда в волокне Iа и длиной мышцы [(FIa = f(L)]-рассматривалась выше (см. рис. 5.8). Этим же способом можно изобразить и характеристику контроллера (набор гомонимных а-мотонейронов); при этом сигналом на входе будет частота импульсов в волокнах Ia (FIa), а на выходе-частота импульсов в связанных с ними α-мотонейронах (Fa). Кривые на рис. 15.6, А дают общее представление о соотношении между экспериментально изменяемой длины мышцы L и частотой разрядов участвующих α-мотонейронов (Fa), когда двигательные волокна перерезаны на уровне вентральных корешков (обратная связь отсутствует). Иными словами, эти характеристики описывают передачу на уровне мышечного веретена и а-мотонейронов.
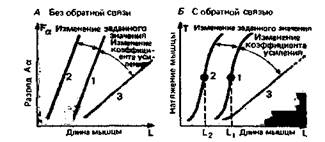
Сначала обратимся к работе схемы без обратной связи (рис. 1 5.6. А), с тем чтобы проанализировать две особенности этих кривых, отражающие важные свойства системы управления в стационарном режиме. В том случае, когда возбудимость а- и γ-мотонейронов изменяется за счет влияния супраспинальных центров и нисходящих из них путей (рис. 15.5), эти кривые сдвигаются параллельно вдоль оси абсцисс (на рис. 15.6, А это переход от линии 1 к линии 2). В принципе такой сдвиг возбудимости может быть вызван уменьшением возбудимости а- либо γ-мотонейронов по отдельности. Однако, исходя из имеющихся экспериментальных результатов, мы должны сделать заключение, что обычно в этом процессе участвуют оба механизма (а - γ-коактивация; см. выше). Параллельный сдвиг характеристик означает новый рабочий диапазон цепи управления;управляемая переменная подстраивается к новому рабочему значению.
Для того чтобы охарактеризовать функцию цепи управления с обратной связью в стационарном режиме (рис. 15.6, А), можно использовать соотношение между напряжением мышцы Τ и ее длиной L (рис. 15.3). Влияние эталонного сигнала - нисходящего возбуждения FH -снова проявляется как сдвиг кривой вдоль координаты L, т. е. от кривой 1 к кри-
340 ЧАСТЬ IV. ПРОЦЕССЫ НЕРВНОЙ И ГУМОРАЛЬНОЙ РЕГУЛЯЦИИ
|
| Рис. 15.6.Характеристики системы управления длиной мышцы при стационарном состоянии. А. Кривые для контроллера, измеренные в условиях без обратной связи и описывающие связь между длиной L и управляющим сигналом Fa. Параллельный сдвиг кривой (от кривой 1 к кривой 2) отражает изменение в эталонном сигнале; изменение угла наклона (от кривой 1 к 3) отражает изменение коэффициента усиления контроллера (красный цвет). Б. Характеристики системы с обратной связью, представленные кривыми длина-натяжение для мышц, находящихся под спинальным управлением. Когда рабочая точка меняется (1 → 2), длина мышцы изменяется от L, к L2. При уменьшении коэффициента усиления (1 → 3) увеличивается податливость мышцы
|
вой 2 при увеличении нисходящего возбуждения FH (рис. 15.6,5). Управляемая переменная (длина мышцы) изменяется в соответствии с эталонным сигналом при переходе к новому рабочему значению L2; данная система работает как следящая. При новом рабочем значении управляемая переменная снова поддерживается на постоянном уровне, несмотря на возмущения, и система работает как регулятор.





