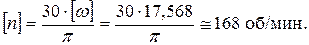Пример выполнения задания № 9
Пример решения задачи № 1
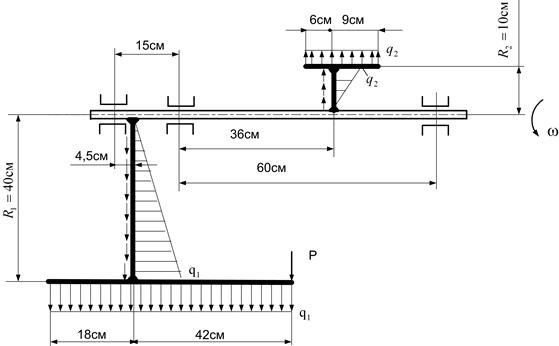
Трехопорная стержневая система, состоящая из вала и присоединенных к нему сосредоточенных масс (см. рис. 9.1), вращается с постоянной угловой скоростью w. Требуется определить допускаемую частоту вращения [ n ]. Материал всех элементов системы – сталь. Допускаемое напряжение [ s ] = 100 МПа. Плотность материала r = 7800 кг/м3. Влиянием собственного веса элементов системы в сравнении с силами инерции пренебречь. Данные для расчета: ℓ;1 = 15 см; с 1 = 60 см; ℓ;2 = 60 см; с 2 = 15 см; R 1 = 40 см; R 2 = 10 см; d = 2 см; а 1 = 0,3 ℓ;1 = 4,5 см; b 1 = 0,3 с 1 = 18 см; а 2 = 0,6 × 60 = 36 см; b 2 = 0,4 с 2 = 6 см. Сосредоточенная масса: m = 1 кг. 1. Вычерчиваем схему конструкции в масштабе и указываем все необходимые размеры (рис. 9.4).
Рисунок 9.4 – Схема вращающейся системы
2. Находим интенсивность распределенной нагрузки горизонтальных участков:
где r = 7800 кг/м3 – плотность стали; R 1 = 0,40 м; R 2 = 0,10 м; 3. Интенсивность распределенной нагрузки радиальных
где 0 £ r 1 £ R 1, 0 £ r 2 £ R 2. 4. Сила инерции сосредоточенной массы m: P = m R 1 w 2. 5. Пользуясь приведенными зависимостями и учитывая исходные данные, находим: q 1 = 6126 × (0,02)2 × 0,40 × w 2 = 0,9802 w 2 Н/м; q 2 = 6126 × (0,02)2 × 0,10 × w 2 = 0,2451 w 2 Н/м; q /1 = 6126 × (0,02)2 × r 1 × w 2 = 2,450 r 1 w 2 Н/м; 0 £ r 1 £ 0,40 м; q /2 = 6126 × (0,02)2 × r 2 × w 2 = 2,450 r 2 w 2 Н/м; 0 £ r 2 £ 0,10 м; Р = 1 × 0,40 × w 2 = 0,40 w 2 Н. Вычерчиваем расчетную схему конструкции (рис. 9.5).
Рисунок 9.5 – Расчетная схема вращающейся системы
6. Рассматриваем консольные части заданной системы, составляем аналитические выражения нормальных сил и изгибающих моментов, пользуясь которыми, строим соответствующие эпюры (рис. 9.6). Аналитические выражения N и Мх для левой консольной части (рис. 9.6, а), составленные по участкам I, II, III, имеют вид:
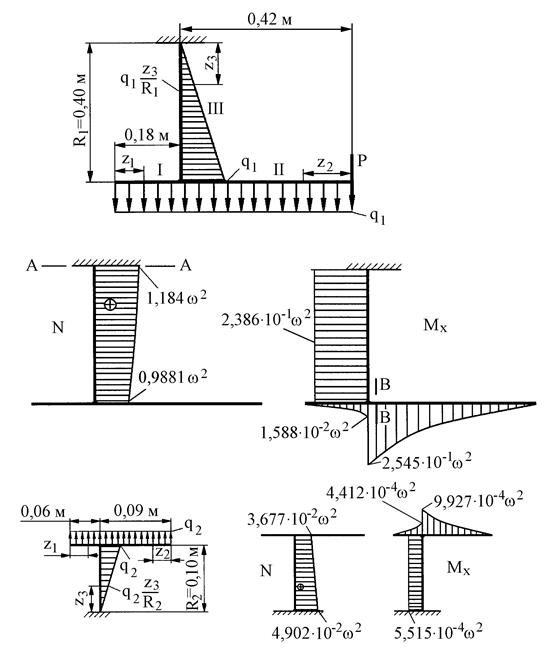
Рисунок 9.6 – Эпюры нормальных сил и изгибающих моментов для консольных частей заданной системы
Результаты вычислений, необходимые для построения эпюр:
Эпюры, построенные по этим данным, приведены на ри- Аналитические выражения N и Мх для правой консольной части (рис. 9.6, б):
Результаты вычислений для построения эпюр:
Эпюры N и Мх для правой консольной части системы приведены на рис. 9.6, б. 7. Вычерчиваем расчетную схему для вала, рассматривая его как неразрезную балку на трех шарнирных опорах. Нагрузки, передаваемые на пролеты балки, определяем по эпюрам N и Мх, построенным на рис. 9.6. Полученная расчетная схема приведена на рис. 9.7, а. 8. Балка один раз статически неопределима. Статическую неопределимость раскроем с использованием уравнения трех моментов. Для его составления выбираем основную систему, врезая шарнир в сечение над промежуточной опорой 1
 

Рисунок 9.7 – Схема к построению эпюры изгибающих моментов для вала
В основной системе построим эпюры изгибающих моментов, предварительно определив реакции опор. Для левого пролета:
Проверка:
Для правого пролета:
Проверка:
Направления реакций опор указаны на рис. 9.7, в. Принимая во внимание найденные значения реакций опор, пользуясь методом сечений, строим эпюры изгибающих моментов, показанные на рис. 9.7, г. Для данной балки уравнение трех моментов имеет вид:
где Пользуясь рисунком 9.7, г, находим:
Из уравнения (*) находим опорный изгибающий момент:
Статическая неопределимость раскрыта. Определим реакции опор в пролетах основной системы от мо-мента М 1:
Реакция
Реакция Находим суммарные значения реакций опор (см. рис. 9.7, б). Для левого пролета:
Для правого пролета:
При вычислении суммарных значений реакций опор слагаемые реакции, направленные вверх, учитывались со знаком (+), а направленные вниз – со знаком (–). Располагая найденными значениями реакций опор, строим окончательную эпюру изгибающих моментов (см. рис. 9.5, д), определяя моменты в характерных сечениях. Проверив правильность построения эпюры Мх по скачкам на величины внешних моментов, сделаем статическую проверку, составив уравнение равновесия для балки по рис. 9.7, а:
что подтверждает правильность значений реакций опор. Погрешность вычислений незначительна и связана с округлениями числовых значений в процессе расчета. С целью выполнения деформационной проверки решения задачи составим универсальное уравнение упругой линии балки по
где у 0 = 0, а угол поворота сечения в начале координат (j 0) найдем из условия отсутствия прогиба в сечении 1:
откуда Подставив это значение в уравнение упругой линии, вычислим прогиб в сечении 2, который равен нулю:
Выражение в скобках незначительно отличается от нуля, что подтверждает правильность найденных значений. 9. Сопоставив эпюры внутренних силовых факторов, построенные для консольных частей заданной системы и ее вала, заметим, что опасными сечениями являются два сечения левой консольной части: А-А и Напряжение в опасной точке сечения А-А:
В сечении В-В:
Сравнив найденные выражения для напряжений, заключаем, что сечение В-В является более опасным. Таким образом, условие прочности составляем для сечения В-В:
где [ s ] = 100 МПа. Следовательно, Допускаемое значение частоты вращения
|


 ,
,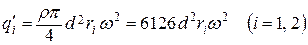 ,
,
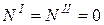 ;
; 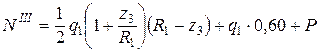 , 0 £ z 3 £ R 1.
, 0 £ z 3 £ R 1. , 0 £ z 1 £ 0,18 м;
, 0 £ z 1 £ 0,18 м; 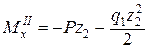 , 0 £ z 2 £ 0,42 м;
, 0 £ z 2 £ 0,42 м;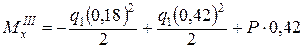 .
.
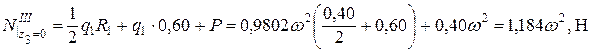 ;
;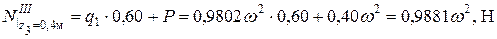 ;
;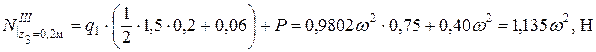 .
.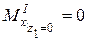 ;
; 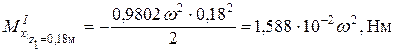 ;
;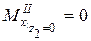 ;
; 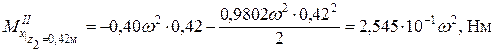 ;
;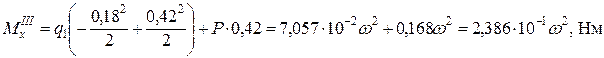 .
. ,
, 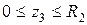 .
.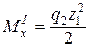 ,
, 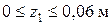 ;
; 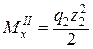 ,
, 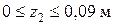 ;
;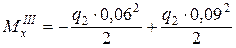 .
. ;
; ;
;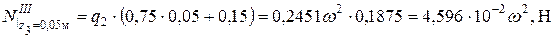 .
.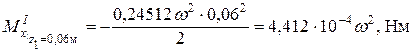 ;
; ;
; .
.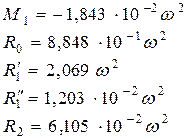
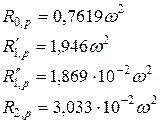
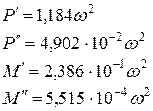
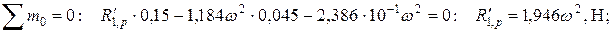
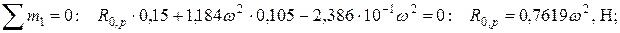
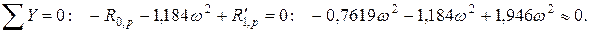

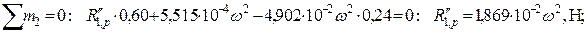
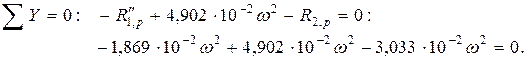
 , (*)
, (*) и
и 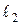 – длины пролетов;
– длины пролетов;  и
и 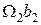 – статические моменты площадей эпюр Мр левого и правого пролетов соответственно относительно левого и правого конца пролета.
– статические моменты площадей эпюр Мр левого и правого пролетов соответственно относительно левого и правого конца пролета.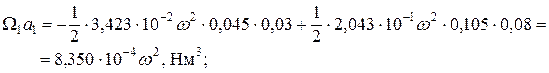
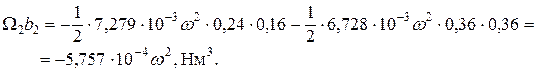
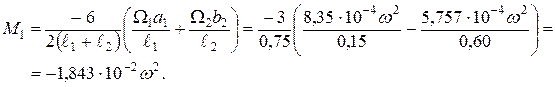
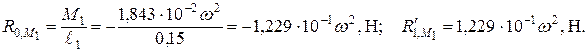
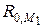 направлена вниз, а
направлена вниз, а 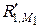 – вверх.
– вверх.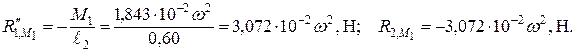
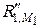 направлена вверх, а
направлена вверх, а 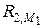 – вниз.
– вниз.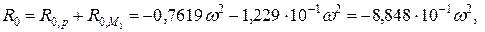 Н (вниз);
Н (вниз);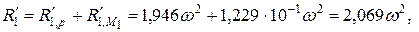 Н (вверх).
Н (вверх).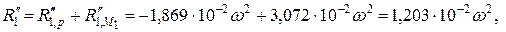 Н (вверх);
Н (вверх);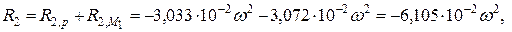 Н (вниз).
Н (вниз).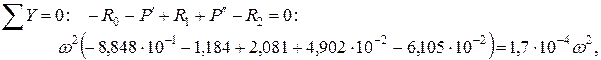
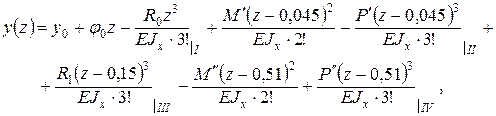
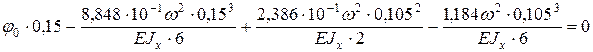 ,
,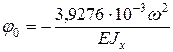 .
.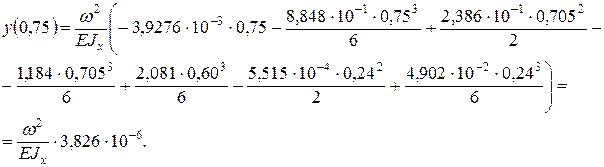
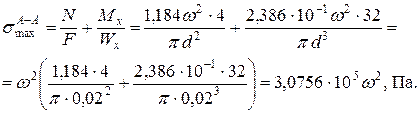
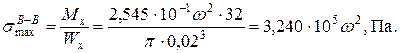
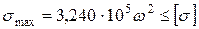 ,
,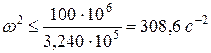 ;
; 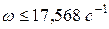 .
.