Повторно-переменных) напряжениях
При действии циклических напряжений прочность вала оценивается по коэффициенту запаса циклической прочности. Можно рекомендовать следующий общий порядок решения задач по определению коэффициента запаса циклической прочности вала при одновременном действии переменных изгибающего и крутящего моментов. 1. Найти средние и амплитудные напряжения циклов изменения нормальных и касательных напряжений:
2. Найти общие коэффициенты снижения циклической проч-ности:
учитывающие результирующее влияние на циклическую прочность вала местного напряжения, размеров детали и качества обработки ее поверхности. Для этого из справочной литературы (по графикам, таблицам, формулам) находят: Кs и Кt – эффективные коэффициенты концентрации напряжений; Кds и Кdt – коэффициенты масштабного фактора; КF – коэффициент качества поверхности; КV – коэффициент поверхностного упрочнения. При нахождении эффективных коэффициентов концентрации используют следующие формулы:
где Необходимые для выполнения задания справочные данные (по вышеперечисленным коэффициентам) приведены в приложении Г. 3. Определить частные коэффициенты запаса циклической прочности – отдельно по нормальным и касательным напряжениям:
где 4. Определить искомый коэффициент запаса циклической прочности вала по формуле
Примечания: 1. Частные и общий коэффициенты запаса должны быть больше единицы. При проектировании валов стремятся, чтобы значения этих коэффициентов находились в пределах 1,3…3,0. 2. При наличии нескольких концентраторов в каком-либо месте вала, например, в случае шпоночного паза и посадки с гарантированным натягом, из двух отношений: Кs / Кds и соответственно
|

 ;
;  ; (9.4)
; (9.4)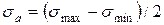 ;
;  . (9.5)
. (9.5) ; (9.6)
; (9.6) , (9.7)
, (9.7) ; (9.8)
; (9.8) , (9.9)
, (9.9) и
и  – эффективные коэффициенты концентрации при «стандартных» размерах вала;
– эффективные коэффициенты концентрации при «стандартных» размерах вала;  – поправочный коэффициент.
– поправочный коэффициент. ; (9.10)
; (9.10) , (9.11)
, (9.11) и
и  – пределы выносливости при симметричном цикле;
– пределы выносливости при симметричном цикле;  и
и  – угловые коэффициенты (прил. Г).
– угловые коэффициенты (прил. Г). . (9.12)
. (9.12)


