Пример решения задачи № 3

 

Для балки (рис. 9.8, а) требуется определить наибольшие нормальные напряжения в опасном сечении и наибольший прогиб точки К при ударе.

Решение: определяем реакции опор и строим эпюру изгибающих моментов М_р от статически приложенной силы Р (рис. 9.8, б, в).

В опасном сечении М ^max = 1 кНм. При этом

ж

е

д

г

в

б

а

Jx = 3460 см4 Wx = 289 см3

 

Рисунок 9.8 – Схема к расчету балки на удар

 

Определяем статический прогиб в точке падения груза. Для этого в месте падения груза (рис. 9.8, г) прикладываем единичную силу и строим «единичную» эпюру М ₁ (рис. 9.8, д).

Перемножаем эпюры М_р и М ₁ по правилу Верещагина и находим:

Определяем статический прогиб балки в точке К. Для этого прикладываем в точке К единичную силу (рис. 9.8, е) и строим «единичную» эпюру М ₂ (рис. 9.8, ж).

Перемножаем эпюры М_р и М ₂ по правилу Верещагина:

Определяем приведенную массу балки по формуле

,

где m ₀ – масса одного метра длины двутавра (для двутавра № 24
m ₀ = 27,3 кг/м); у (z) – функция, определяющая вид упругой линии балки при ударе; у ₀ – значение функции y (z) в точке падения груза.

На рисунке 9.8, б приведена система координат (0 < z <5 м) и приблизительная форма упругой линии балки, которую можно описать уравнением

.

Отсюда

Определяем коэффициент динамичности:

.

Наибольшее нормальное напряжение в опасном сечении при
ударе:

.

Наибольший прогиб в точке К при ударе:

.

Рекомендуемая литература

 

1. Дарков, А.В. Сопротивление материалов / А.В. Дарков,
Г.С. Шпиро. – М.: Высшая школа, 1969. – С. 589-595, 624-627.

2. Алмаметов, Ф.З. Расчетные и курсовые работы по сопротивлению материалов / Ф.З. Алмаметов, С.И. Арсеньев, С.А. Енгалычев и др. – М.: Высшая школа, 1992. – С. 215-225.

3. Когаев, В.П. Прочность и износостойкость деталей машин / В.П. Когаев, Ю.Н. Дроздов. – М.: Высшая школа, 1991. – 319 с.

4. Серенсен, С.В. Несущая способность и расчеты деталей на прочность: справочное пособие / С.В. Серенсен, В.П. Когаев,
Р.М. Шнейдерович. – М.: Машиностроение, 1975. – 488 с.

5. Долинский, Ф.В. Краткий курс сопротивления материалов / Ф.В. Долинский, М.Н. Михайлов. – М.: Высшая школа, 1988. –
С. 331-351.

6. Якунин, Л.С. Сопротивление материалов переменным нагрузкам: методические указания к практическим занятиям / Л.С. Якунин. – Орел: ОрелГПИ, 1993. – 28 с.
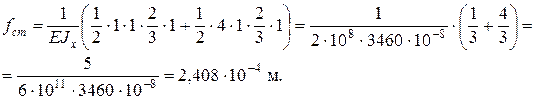