Задача № 2. Стальной стержень тонкостенного открытого профиля (рис

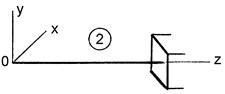
Стальной стержень тонкостенного открытого профиля (рис. 10.2), имеющий опорные закрепления по концам согласно одному из вариантов (рис. 10.3), находится под действием заданной статической нагрузки.

 

Рисунок 10.2 – Схема нагружения стержня

 

Требуется:

1) определить площадь, положение центра тяжести и вычислить значения главных центральных моментов инерции поперечного сечения стержня;

2) определить положение центра изгиба (главного полюса) и вычислить значение секториального момента инерции сечения;

3) вычислить значение изгибно-крутильной характеристики жесткости стержня;

4) записать уравнения метода начальных параметров и определить по заданным граничным условиям неизвестные начальные параметры. Записать уравнения углов закручивания j, бимоментов В, изгибно крутящих моментов М_w, моментов чистого кручения М_к;

5) построить эпюры поперечных сил, изгибающих моментов, моментов чистого кручения, изгибно-крутящих моментов, бимоментов и углов закручивания;

6) построить эпюры распределения нормальных и касательных напряжений в поперечном сечении с наибольшим бимоментом.

Принять: Е = 2*10^5 МПа, G = 8*10^4 МПа.

Толщина стенки постоянна для всех элементов профиля –
b = 0,05* b, где b – ширина полки.

Исходные данные к задаче № 2 принять в соответствии с заданным вариантом по таблице 10.2.

 

Таблица 10.2 – Данные к задаче № 2

№ строки	I	II	III
Размеры стержня (рис. 10.2)	№ схемы опирания (рис. 10.3)	Координаты точек приложения и значения нагрузок (кН)
ℓ;,м	b, см	h, см	a 1 ℓ;	a 2 ℓ;	c h	s b	P 1	P 2	P 3	P 4
	1,0				0,2	0,8	0,0	0,9		-	1,2	-
	1,2				0,4	0,6	0,2	0,8	-	1,9	-	1,1
	1,4				0,6	0,4	0,4	0,7	1,8	-	1,4	-
	1,6				0,8	0,2	0,6	0,6	-	1,7	-	1,3
	1,8				0,6	0,3	0,8	0,5	1,6	-	1,6	-
	2,0				0,4	0,7	1,0	0,4	-	1,5	-	1,5
	2,2				0,2	0,6	0,0	0,3	1,4	-	1,8	-
	2,4				0,4	0,8	0,2	0,2	-	1,3	-	1,7
	2,6				0,6	0,8	0,4	0,1	1,2	-	2,0	-
	2,8				0,8	0,4	0,6	0,0	-	1,1	-	1,9

 

 

Примечание: опорные закрепления на рис. 10.2 показаны условно и должны приниматься согласно заданному варианту по рис. 10.3.

 

 

 

 

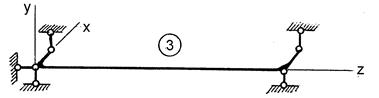
Рисунок 10.3 – Схемы опорных закреплений

 

Примечания:

1. В заделанном сечении (варианты 1, 2) исключены все виды смещений.

2. При шарнирном опирании (вариант 3) считать, что поворот опорных сечений относительно оси z исключен, но депланация может развиваться свободно.