Метод начальных параметров
Начальными параметрами называют геометрические и силовые факторы, взятые в начале координат: Последовательно дифференцируя (10.30), при условии отсутствия распределенной нагрузки (j * = 0) получим:
Тогда согласно (10.36) и при учете (10.28):
Причем
Полагая z = 0, из (10.30), (10.37) – (10.39) находим:
Подставив выражения (10.40) в (10.30), (10.37), (10.38), получаем уравнения метода начальных параметров для участка I стержня:
Уравнение углов закручивания для любого n -го участка записывается аналогично универсальному уравнению изогнутой оси балки. Для стержня постоянного сечения, не имеющего скачков бимоментов, углов поворота и их производных, оно имеет вид:
где D Мi – скачки крутящих моментов, равные внешним моментам; Аналогично выражению (10.42), с помощью уравнений (10.41) могут быть записаны выражения для остальных величин, так как функции влияния, входящие в (10.41), известны. Если к стержню приложена распределенная закручивающая нагрузка постоянной интенсивности (m = const), то к правой части уравнения (10.42) добавится слагаемое:
где а i – расстояние от начала координат до сечения, с которого начинается распределенная нагрузка. Общие выражения для Неизвестные начальные параметры определяют из граничных условий по концам стержня.
10.2.7 Определение напряжений в общем случае действия сил на тонкостенный стержень
В общем случае нагружения тонкостенного стержня открытого профиля при вычислении напряжений используется принцип суперпозиции. Формула нормальных напряжений имеет вид:
где N – нормальная сила; Мх, Му – изгибающие моменты относительно главных центральных осей; В – бимомент; х, у – декартовы координаты точки, в которой определяется напряжение; w – секториальная координата; F – площадь сечения; Jx и Jy – главные центральные моменты инерции сечения; Jw – секториальный момент инерции. Полное касательное напряжение в исследуемой точке сечения определяется как алгебраическая сумма касательных напряжений от действия поперечных сил Qx, Qy, момента чистого кручения Мк, изгибно-крутящего момента Мw:
где
d – толщина стенки профиля; Напряжения tк определяются в крайних точках по (10.1), а tw – по (10.18). Внутренние силовые факторы: бимомент В, момент чистого кручения Мк и изгибно-крутящий момент Мw, – не могут быть найдены методом сечений, то есть по условиям равновесия отсеченной части стержня. Для их определения используются зависимости (10.36).
|

 ,
,  , В 0,
, В 0,  .
. (10.37)
(10.37)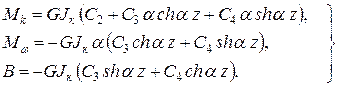 (10.38)
(10.38)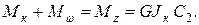 (10.39)
(10.39) (10.40)
(10.40)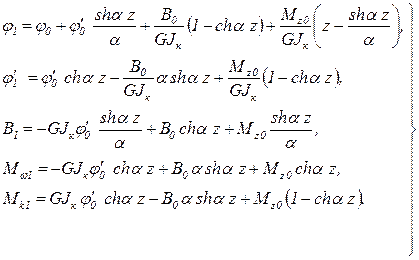 (10.41)
(10.41) (10.42)
(10.42) (10.43)
(10.43) могут быть получены также путем последовательного дифференцирования уравнения (10.42) при учете зависимостей (10.36).
могут быть получены также путем последовательного дифференцирования уравнения (10.42) при учете зависимостей (10.36). (10.44)
(10.44) (10.45)
(10.45) – напряжения, определяемые по формуле Д.И. Журавского:
– напряжения, определяемые по формуле Д.И. Журавского: (10.46)
(10.46) – статические моменты отсеченной части сечения для точки, в которой определяются напряжения.
– статические моменты отсеченной части сечения для точки, в которой определяются напряжения.


