Пример решения задачи № 2
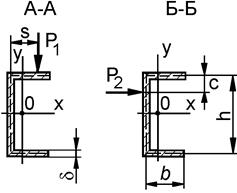
Тонкостенный стальной стержень открытого профиля в форме швеллера, закрепленный по концам согласно рис. 10.12, находится под действием двух сосредоточенных сил Р 1 и Р 2, приложенных соответственно в сечениях А-А и В-В. (Записать текст задания по п. 10.1). Данные: ℓ = 3 м; b = 10 см; h = 20 см; а 1 = 0,3 ℓ;; a 2 = 0,7 ℓ;; c = 0,2 b; Повороты опорных сечений исключены, депланация не стеснена. Решение: 1–2. Рассмотрим поперечное сечение стержня и определим его геометрические характеристики (см. рис. 10.5). Площадь сечения: Координата центра тяжести относительно оси у 1 (см. рис. 10.5):
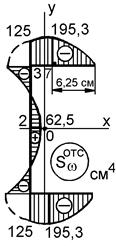
Дальнейший расчет выполняется согласно методике, изложенной в примере п. 10.2.4 (расчет дать полностью). Найденные значения главных центральных моментов инерции: Jx = 2667 см4; Jy = 417 см4. Положение центра изгиба (центра кручения, главного полюса) показано на рис. 10.6, а, а эпюра главных секториальных координат построена на рис. 10.6, б. Путем умножения этой эпюры самой на себя найдено значение секториального момента инерции сечения: Jw = 29167 см4. 3. Определим изгибно-крутильную характеристику жесткости стержня.
Рисунок 10.12 – Схема опирания и нагружения стержня
Предварительно находим геометрическую характеристику крутильной жесткости Jк по формуле (10.4):
где размеры стенки (hc, dc) и полки (hn, dn) швеллера определены по Жесткость сечения при свободном кручении:
Секториальная жесткость тонкостенного сечения:
Изгибно-крутильная жесткость:
4. Записываем универсальные уравнения метода начальных параметров при стесненном кручении (см. (10.41) и (10.42)):
Для заданной расчетной схемы (рис. 10.12) имеем:
Причем координата центра кручения ах = -3,75 см найдена в примере п. 10.2.4. Уравнения метода начальных параметров в данном случае принимают вид:
Входящие в это уравнение начальные параметры определим из граничных условий на правом конце стержня (при z = ℓ;): j (ℓ;) = 0, B (ℓ;) = 0. В развернутой форме граничные условия имеют вид:
Решая полученную систему алгебраических уравнений, находим:
Подставив найденные значения в уравнения, окончательно
5. Построим эпюры внутренних силовых факторов и углов закручивания стержня. Находим реакции опор стержня от вертикальной силы Р 1 и горизонтальной силы Р 2:
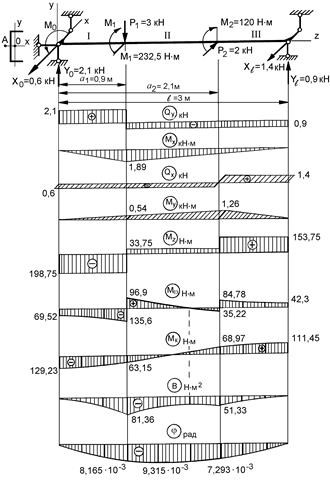
Пользуясь методом сечений, строим эпюры Qy, Mx, Qx, My, Mz
Рисунок 10.13 – Расчетная схема и эпюры для тонкостенного стержня Таблица 10.4 – Значения Мw, Мк, В и j для построения эпюр
Для построения эпюр Мw, Мк, В и j производим вычисления, результаты которых заносим в таблицу 10.4. По найденным значениям строим эпюры Мw, Мк, В (см. 6. Построим эпюры распределения нормальных и касательных напряжений в сечении с наибольшим бимоментом. В этом сечении:
Определим законы распределения нормальных напряжений от действия каждого внутреннего силового фактора:
Пользуясь данными выражениями, строим эпюры нормальных напряжений от действия каждого внутреннего силового фактора
а б в г
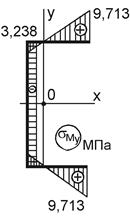
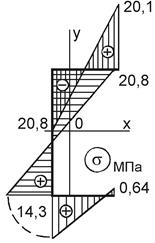
Рисунок 10.14 – Эпюры нормальных напряжений
Суммируя напряжения от действия Мх, Му и В, строим результирующую эпюру нормальных напряжений (см. рис. 10.14, г). Касательные напряжения в данном поперечном сечении связаны с внутренними силовыми факторами Qx, Qy, Mw, Mk. По формуле Д.И. Журавского имеем:
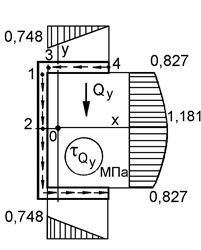
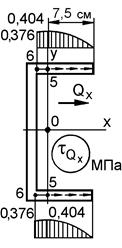
Эпюры напряжений tQx и tQy строим по характерным точкам, вычислив значения статического момента отсеченной части сечения для этих точек (рис. 10.15).
а б в г Рисунок 10.15 –Построение эпюр касательных напряжений
Для определения секториальных касательных напряжений tw построим эпюру Эпюра
Например,
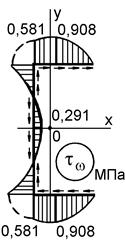
Эпюра Напряжения tw определяем по формуле (10.18):
Отсюда следует, что эпюра tw подобна эпюре Напряжения tw в характерных точках (см. рис. 10.15, г):
Эпюра tw представлена на рис. 10.15, г. Следует иметь в виду, что по формуле (*) определяют напряжения в продольных сечениях стержня. Причем tw положительны, если направлены в отрицательном направлении оси z (при действии по продольному сечению отсекаемой части стержня, получаемой при обходе контура против хода часовой стрелки). В поперечном сечении направления секториальных касательных напряжений определяют по закону парности. На эпюре tw (см. Касательные напряжения чистого кручения tк, в отличие от напряжений tw, tQx, tQy, распределенных по толщине профиля равномерно, равны нулю в точках средней линии профиля и достигают наибольших значений в крайних точках, принадлежащих длинным сторонам прямоугольников, на которые разбивают сечение. При этом считают, что по толщине сечения tк распределяются по линейному В данном случае по формуле (10.1) имеем:
Элементарные касательные усилия в каждом прямоугольнике образуют моменты, направленные по ходу часовой стрелки, на что указывает знак (–). Наибольшие касательные напряжения возникают в точке стенки, ближайшей к центру тяжести сечения:
Эти напряжения заметно меньше наибольших нормальных напряжений (см. эпюру s на рис. 10.14, г). Рекомендуемая литература
1. Александров, А.В. Сопротивление материалов: учебник для вузов / А.В. Александров, В.Д. Потапов, Б.П. Державин. – М.: Высшая школа, 1995. – С. 306-340. 2. Бояршинов, С.В. Основы строительной механики машин: учебное пособие для студентов вузов / С.В. Бояршинов. – М.: Машиностроение, 1973. – С. 5-59. 3. Варданян, Г.С. Сопротивление материалов с основами теории упругости и пластичности / Г.С. Варданян, В.И. Андреев, Н.М. Атаров, А.А. Горшков. – М.: Издательство АСВ, 1995. – С. 178-182, 4. Сопротивление материалов: учебник для вузов / Под редакцией А.Ф. Смирнова. – М.: Высшая школа, 1975. – С. 311-342. 5. Сборник задач по сопротивлению материалов: учебное пособие для вузов / Под редакцией А.В. Александрова. – М.: Стройиздат, 1977. – С. 216-238. 6. Миролюбов, И.Н. Пособие к решению задач по сопротивлению материалов / И.Н. Миролюбов, С.А. Енгалыдев, Н.Д. Сергиевский и др. – М.: Высшая школа, 1985. – С. 227-240.
Литература
1. Александров, А.В. Сопротивление материалов / А.В. Александров, В.Д. Потапов, Б.П. Державин. – М.: Высшая школа, 1995. – 560 с. 2. Феодосьев, В.И. Сопротивление материалов / В.И. Феодосьев. – М.: Наука, 1996. – 512 с. 3. Смирнов, А.Ф. Сопротивление материалов / А.Ф. Смирнов, А.В. Александров, Н.И. Монахов и др. – М.: Высшая школа, 1975. – 480 с. 4. Алмаметов, Ф.З. Расчетные и курсовые работы по сопротивлению материалов / Ф.З. Алмаметов, С.И. Арсеньев, С.А. Енгалычев и др. – М.: Высшая школа, 1992. – 320 с. 5. Чернышев, В.И. Методические указания по выполнению расчетно-проектировочных работ по курсу «Сопротивление материалов с применением вычислительной техники», часть 1 / В.И. Чернышев, Л.С. Якунин, И.А. Бурнашев, Е.Т. Кобяков и др. – Орел: ОФ ВЗМИ, 1988. – 48 с. 6. Кобяков, Е.Т. Задания и методические указания к расчетно-проектировочным работам по сопротивлению материалов, часть 2 / Е.Т. Кобяков, И.А. Бурнашев, В.И. Чернышев, О.П. Шакулин и др. – Орел: ОФ МИП, 1992. – 52 с. 7. Александров, А.В. Сборник задач по сопротивлению материалов / А.В. Александров, Б.П. Державин, Б.Я. Лащеников и др. – М.: Стройиздат, 1977. – 335 с. 8. Миролюбов, И.Н. Пособие к решению задач по сопротивлению материалов / И.Н. Миролюбов, С.А. Енгалычев, Н.Д. Сергиевский и др. – М.: Высшая школа, 1985. – 399 с. 9. Долинский, Ф.В. Сопротивление материалов: Методические указания и контрольные задания для студентов-заочников механических, машиностроительных и транспортных специальностей высших учебных заведений / Ф.В. Долинский, М.Н. Михайлов. – М.: Высшая школа, 1990. – 80 с. 10. Кобяков, Е.Т. Расчетные работы по сопротивлению материалов (задания и методические указания), часть 1 / Е.Т. Кобяков, В.И. Чернышев. – Орел: ОрелГТУ, 1996. – 68 с. 11. Кобяков, Е.Т. Расчетные работы по сопротивлению материалов (задания и методические указания), часть 2 / Е.Т. Кобяков, В.И. Чернышев. – Орел: ОрелГТУ, 1996. – 93 с. 12. Чернышев, В.И. Применение метода конечных разностей в задачах изгиба стержней / В.И. Чернышев. – Орел: ОрелГТУ, 1998. – 25 с. 13. Чернышев, В.И. Преобразование Лапласа и его применение в теории изгиба стержней / В.И. Чернышев. – Орел: ОрелГТУ, 2001. – 36 с. 14. Кобяков, Е.Т. Построение эпюр внутренних силовых факторов для плоских статически определимых стержневых систем / Е.Т. Кобяков. – Орел: ОФ МИП, 1993. – 39 с. 15. Кобяков, Е.Т. Определение перемещений в статически определимых балках при прямом поперечном изгибе / Е.Т. Кобяков. – Орел: ОГПИ, 1994. – 34 с. 16. Кобяков, Е.Т. Расчет тонкостенных стержней открытого профиля / Е.Т. Кобяков. – Орел: ОрелГТУ, 1998. – 44 с. 17. Кобяков, Е.Т. К расчету статически определимых балок ступенчато-переменного сечения / Е.Т. Кобяков. – Орел: ОГПИ, 1994. – 24 с. 18. Кобяков, Е.Т. Определение геометрических характеристик плоских сечений с применением ЭВМ / Е.Т. Кобяков, И.С. Шуев. – Орел: ОФ МИП, 1993. – 26 с. 19. Чапка, А.М. Расчетно-проектировочные работы на программируемых микрокалькуляторах / А.М. Чапка. – М.: Машиностроение, 1988. – 144 с. 20. Кобяков, Е.Т. К вопросу определения усилий и перемещений в элементах стержневых систем / Е.Т. Кобяков // Строительство и архитектура. – 1979. – № 7. – С. 39-43. 21. Спицына, Д.И. Строительная механика стержневых машиностроительных конструкций / Д.И. Спицына. – М.: Высшая школа, 1977. – 248 с. 22. Кобяков, Е.Т. Экспериментальное определение осевых моментов инерции тел и плоских сечений методом колебаний / Е.Т. Кобяков, О.И. Квятковский, И.С. Шуев. – Орел: ОФ МИП, 1992. – 20 с. 23. Шуп, Т. Решение инженерных задач на ЭВМ / Т. Шуп. – М.: Мир, 1982. – 238 с. 24. Александров, А.В. Основы теории упругости и пластичности / А.В. Александров, В.Д. Потапов. – М.: Высшая школа, 1990. – 400 с. 25. Деч, Г. Руководство к практическому применению преобразования Лапласа и Z-преобразования / Г. Деч. – М.: Наука, 1971. – 26. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся вузов / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 1986. – 544 с. 27. Писаренко, Г.С. Справочник по сопротивлению материалов / Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. – Киев: Наукова думка, 1975. – 704 с. 28. Дьяконов, В.П. MATHCAD 8/2000. Специальный справочник / В.П. Дьяконов. – СПб.: ПИТЕР, 2000. – 592 с. 29. Сборник задач по сопротивлению материалов / Под редакцией А.С. Вольмира. – М.: Наука, 1984. – 408 с.
|

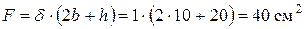 .
.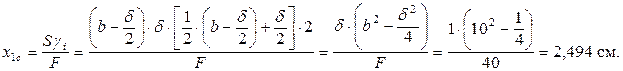


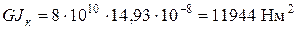 .
.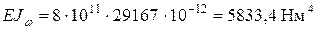 .
.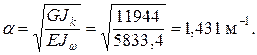
 ;
;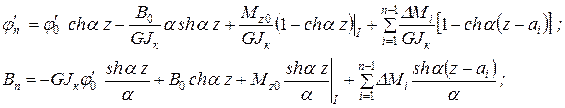

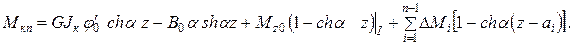

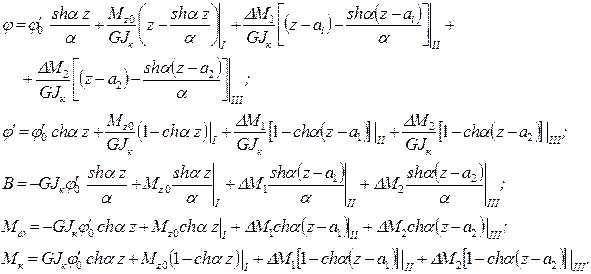
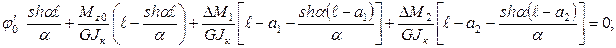

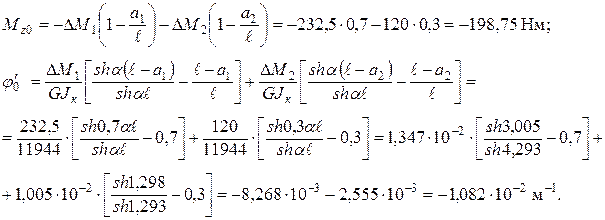
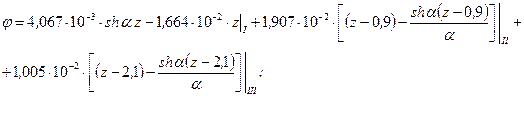

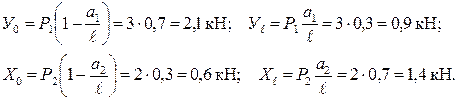
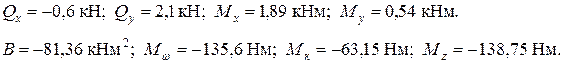
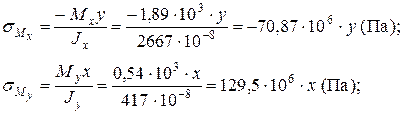



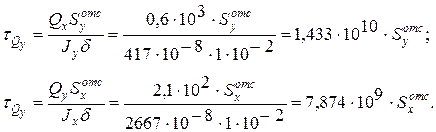
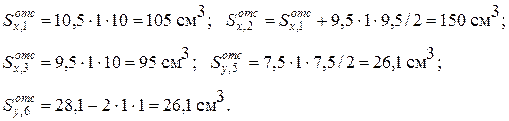
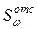 , воспользуясь эпюрой w (см. рис. 10.6, б).
, воспользуясь эпюрой w (см. рис. 10.6, б). .
. ;
;
 . (*)
. (*)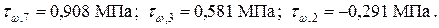
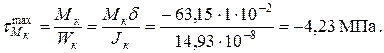
 .
.


